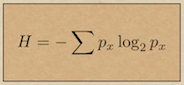Information Theory for Understanding Living Systems

Of course, information theory lies at the heart of an information-based understanding of life. This theme explains and develops the information theoretic concepts needed for the other themes and incorporates the concepts that have been inspired by an information-focussed study of life.

Usually, information theory starts with Claud Shannon's mathematical description of communication (the icon image for this theme is Shannon's equation defining information entropy). But for our purpose, we have to dig deeper. Although Shannon's communications theory is very valuable in some aspects of biology, such as calculating the information transcribed from DNA (e.g. see these calculations), it is not really a theory of information; rather it is just a theory of the statistical basis of information transfer. In dealing with the information basis of life, we think it necessary to consider the role of information in forming the structures of life and that leads us straight into two aspects that Shannon (and followers) resolutely reject. The first is that Shannon's theory does not accept the idea of information content. As they formulate the idea, information strictly characterises a relationship between a source and a receiver of signals, so it is relational and cannot be intrinsic to any system: it is not a property of a thing and cannot be contained. The second is that it says nothing about meaning: information in the Shannon sense is not interpreted and its consequences are of no concern within the theory. This is not a weakness or error of the theory, it is just the consequence of drawing a clear boundary around its scope: something that gives it rigour, which is of course a strength. However, to deal with the information basis of life, we think we need to deal with these aspects which lie beyond the scope of Shannon's theory, so we have to look more broadly for inspiration. In particular, we will need this to examine the relations between the structure and function of biological systems and that requires a more general understanding of information.

This more general understanding is mainly attributable to Luciano Floridi, but has been substantially expaned by Keith Farnsworth to give a set of connected definitions for information-related concepts.

We begin with data, the element of which is a single binary difference: yes/no, on/off or black/white. This single difference (on is different from off in one single respect) is the smallest element of data, so a set of n differences constitutes n-bits of data. That is to say it takes n bits of data to fully describe something that can be decomposed into a set of n binary differences.

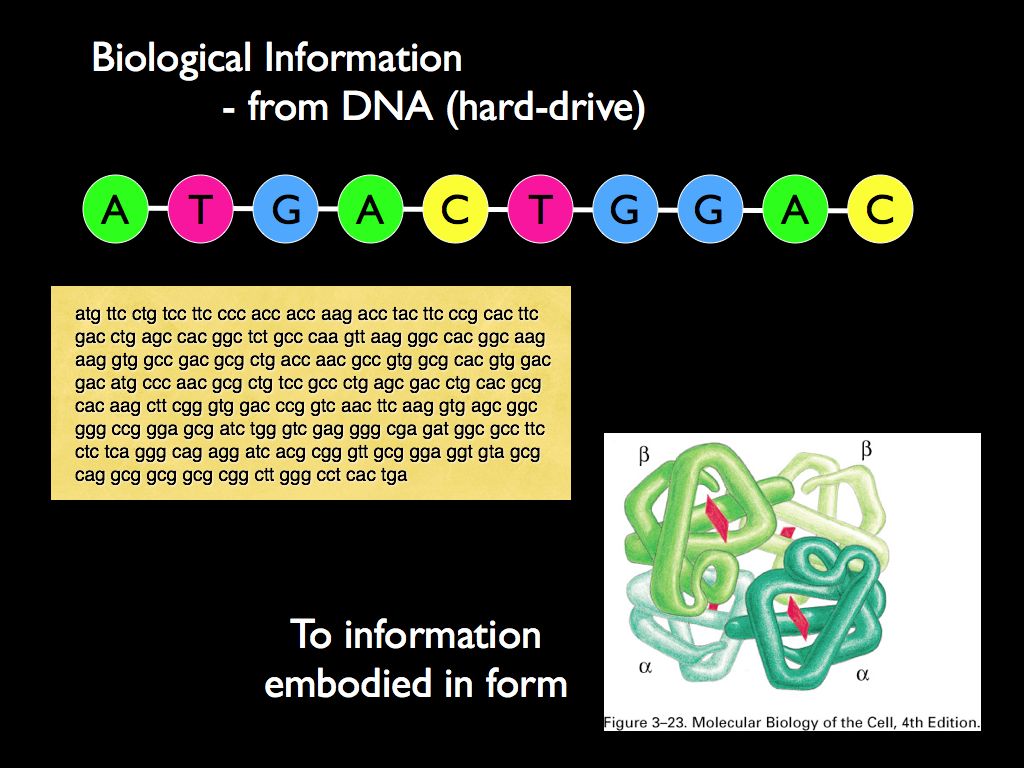
Data is the ‘raw material’ of physical information. This is familiar to us as electronic computers store information in the form of strings of binary data. What the stored data actually consists of is a set of binary differences making a striped pattern in some material substance (e.g. the magnetisation of a thin disk of iron oxide). A DNA molecule stores data as a base-4 set of differences among the nucleic acids (A,G,C, and T), also making a pattern like a string of beads which can be ‘read’. The data is amenable to Shannon’s mathematical information theory and all that follows from it. But more generally, the pattern formed by the stored data is a configuration of matter in time and space that we say embodies and instantiates the data. By the same thinking, we can interpret any material object as a form in space and time defined by a pattern of differences: that is the object instantiates data. 

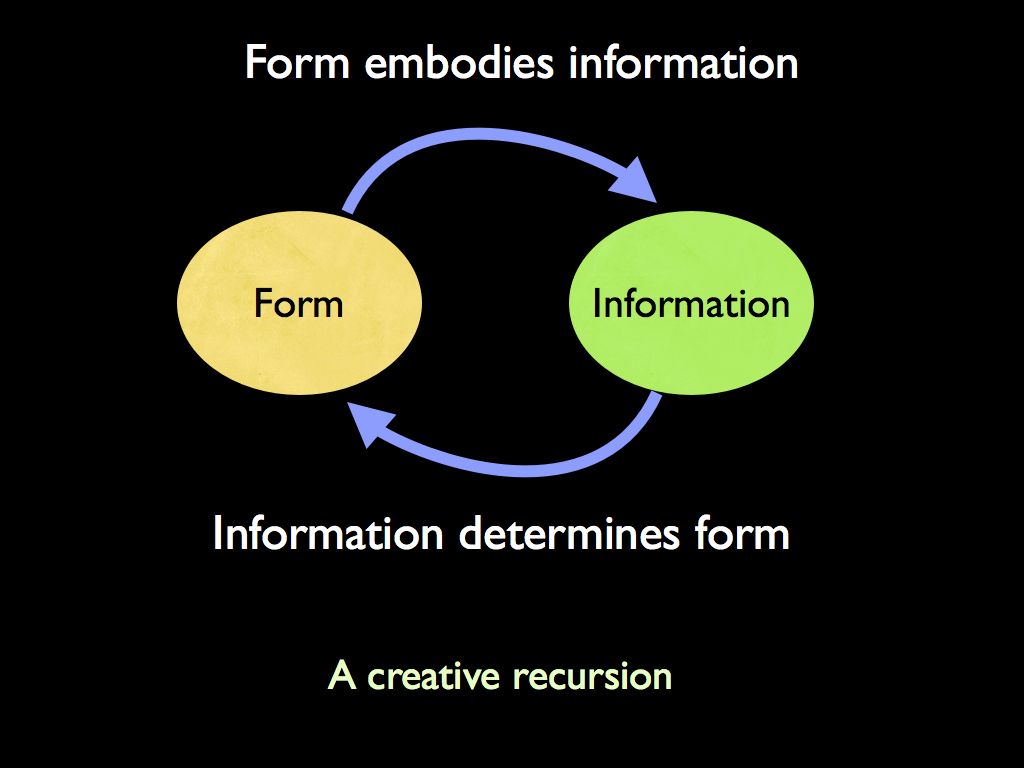
Data instantiating the form of an object is equivalent (reversibly) with the object’s form embodying the data. Thus we can speak not only about data describing the object, but also the object being data: a pattern of matter in space and time. Very often the form of an object is functional, for example the shape of an enzyme molecule determines its function (indeed this is a general truth about molecules). 

Perhaps the most useful, but misunderstood result of information theory is the concept of information entropy which is a measure of the number of ways an assembly of components can be arranged. This enables us to calculate the amount of information that can be embodied in an assembly. It applies to every kind of assembly from DNA sequences to whole ecosystems. Entropy is particularly useful in calculating information conveyed by random processes.

The definition of physical information to which Floridi points us is that of 'well formed and meaningful data'. This raises the difficult problem of ‘meaningful’, usually considered in the context of messages. In its most general sense, we take meaningful to be identical with ‘functional’, where function refers to the potential to cause a change in information pattern. We can think of meaningful data (for example a functional gene) as being able (in conjunction with an appropriate process) of creating a new pattern (for example a protein that the DNA codes for).

In mathematical information theory (which in fact deals only with the statistics of data), meaning is never referred to (this blindness to meaning is one of its founding axioms). When we refer to information, we mean well formed and functional data, in the sense that the pattern it consititutes may modify (or form) further pattern in matter (or energy): changing the distribution of matter in space and time. This is memorably captured in the phrase of Gregory Bateson: information is “a difference which makes a difference” (even though that is not really what he meant at the time)*. These ideas are taken further in the Philosophy theme, here we concentrate on the application of mathematical information theory (a the theory of data, without reference to meaning), supplemented by a separate theory of function relevant to biological systems.

* Bateson was talking about cognition and saying that of all differences in the environment, only those that make a difference to the organism can be considered as information. His oft-quoted slogan is frequently  misunderstood as implying that information is in gerenal functional (i.e. making a difference), but Bateson rather meant the opposite of that. Again, see our set of connected definitions for further comment.

Biological Implications of the Mathematical Theory of Information

Shannon's theory of communication has been successfully used to better understand the cybernetics (i.e. informational) mechanisms and consequences of molecular biology, particularly DNA and RNA coding (information storage), transcription (communication) and gene regulatory networks (computation). All these aspects are drawn together in our Molecular Biology Theme which highlights work by Thomas Schneider and Christoph Adami in particular. This naturally leads into the contribution that such understanding provides for answering the question of how life originated (especially the RNA-first hypothesis), for example the puzzle caused by the sequence paradox.

The deeper (Aristotelean) theory of 'information as embodied in form' has helped us begin to understand the control architecture of biological systems and most excitingly, how autonomy and even free will emerge from autopoietic systems.

The Shannon theory (often termed the mathematical theory of information) starts with a rather clever insight into what we learn from receiving information, literally bit by bit. If you don't know what that is, we recomend you start with our page on information uncertainty. The next step in understanding the theory is to get to grips with its central concept: entropy (which is so important that you will find many of our other pages refer to it as well). The theory is applied in molecular biology, as I said before, but also plays a central role in understanding and quantifying biodiversity, in particular the formation of metrics for biodiversity. Finally, we are gradually moving towards an information theoretic understanding of the quite elusive concepts of causation and autonomy, for example through metrics such as Integrated Information Theory, which are introduced on those pages.


Introductions to Information Theory for Biologists

Adami C. 2016 What is information? Phil. Trans. R. Soc. A 374: 20150230. http://dx.doi.org/10.1098/rsta.2015.0230