Causation: why things happen
A short article by Keith Farnsworth, July 2019 (still under construction).Ancient and modern ideas about causation.
Aristotle separated the notion of cause into four categories: material, efficient, formal, and ultimate. These are not alternative modes of causation: in his account, causation involves all four because they are the four natures (or aspects) of causation. Most modern philosophers seem to pay little attention to this as by far the majority of their current work concerns efficient cause only, which is usually taken to be the only true cause (many believe the other three were not really causes at all).
Efficient Cause is the 'dynamic' in causation: what changes one thing to another by actual physical processes and is closest (of the four) to what we, these days, usually mean by proximate cause: the direct physical process that results in an observed effect. According to most readings, efficient cause comes from an extrinsic agency: In the classic example, it is the cue ball that strikes the red ball, causing it to move. In one of Aristotle's own examples, it is the carpenter who carves a bowl from a block of wood (causing the wooden block to become a bowl); in a modern engineering example, it is the current passing through the terminals of a lamp (l.e.d. of course) that cause it to glow. Not that things have to be moving: it is also the girder that causes the bridge to resist falling down.
For a moment think of that girder. It is made of steel, so very strong. If it had been made of cheese, well, it would no doubt fail and this difference, according to Aristotle, is attributable to the material aspect of cause. Not only does the girder have to be in the right place to save the bridge, it has to be made of the right stuff. Notice I mentioned it being in the right place to do its job. This is a matter of its spatio-temporal relation to the rest of the bridge (and world). A little more broadly, if we include its shape - all its matter being in a particular place at a particular time - then we have the formal aspect of cause i.e. cause that depends on the form of the object for its action.
Ultimate cause
This is simply rejected in modern science because for there to be an ultimate cause, there must be a purpose and one of the tenets of modern science is that there is no purpose to nature (a position adopted after long struggling against religious authorities). This is easy to accept regarding the non-living, but it is hard to avoid the idea that living things do have a (self-defined) purpose. We might argue that for there to (hypothetically) be a purpose for anything, it must arise from some entity having a goal and this is only possible if the entity has an autonomous identity; but then all living things do have that. Ultimate cause could only have meaning for an autonomous entity because only that can have a goal, since a goal is a source of information that is independent of everything that is exogenous to the entity. Mainstream scientists will respond that organisms only seem (anthropocentrically) to have goals: it is an illusion. They usually believe this is tantamount to admitting teleological thinking which is taboo and a serious faux-pas. We will have to return to ultimate cause later in the article.


Empiricism heralds the modern age
David Hume, one of the founders of empiricism, in his 1739 treatise, argued that all we can gain from observing `nature' is the frequency with which one event follows another: we cannot directly observe (or experience) cause. This means that cause can only ever be as much as `suspected' from observation of `regularities' in our empirical observations. This 'regularity' theory breaks down under several philosophical challenges and has been abandoned by most professional philosophers. Notice, though, that if we can only consider what we observe, then Aristotle's ultimate cause becomes permanently inaccessible and can be left out of further inquiry (which is largely what has happened ever since).
Bertrand Russell (1913) went further, claiming that cause (in general) was essentially a figment of our imagination: events are connected, but not in a specifically causal way because, he argued, cause is necessarily directional and the physics he was aware of at the time explained phenomena in terms of strictly symmetric relations (no preferred direction). Modern physics provides good reasons why physical relations are not always symmetric (e.g. the second law of thermodynamics and the `arrow of time', so Russell's main argument is not well supported, but his conclusion still has its followers in the field. One important challenge we may consider shortly is whether cause really does necessitate a time asymmetry.
Physics
Still, it seems right that physics should provide an explanation of causation. In the physical (real) world, cause is always the result of the action of a physical force (usually, but not necessarily on matter), is it not?. We know all the physical forces and how they act, also we know how matter responds (the effect). According to the 'physicalist' interpretation, there is no room for debate here, if real things happen in the real world, then physical forces lie behind them. More precisely, the physical mechanism behind cause is a transfer of a conserved quantity (energy, momentum or something more exotic like charge or spin) in a material system. The modern version of this idea is causal process theory (Salmon,1984; Dowe,2000) which posits that there must be a spatio-temporally continuous connection between one thing X and another Y involving the transfer of energy, momentum (or other conserved quantity) for X to cause Y. Physics most certainly deals with material systems that can take a number of states and transition between them, so this is clearly good for efficient cause by state-constraint (see box below). It certainly cannot address ultimate cause, though it may encompass material cause, it struggles with formal cause because that is specifically about the spatio-temporal relation among components of a system, so whilst in principle using locations and vectors for forces it can handle formal cause, it practice it is too complicated a job for all but the very simplest of systems (e.g. three bodies influencing one another by gravity). Still, when it comes to the physical world of material objects and their interactions, the harnessing of physical forces underlies efficient causation (and its atomic-level manifestation of material causation). The transference theories such as causal process theory are capable of explaining signal transformation via the details of the mechanisms in e.g. mechanical or electrical systems, but the idea of ontological cause (below) seems to be beyond their scope in principle. Despite this, it is worth noting that the physicalist interpretation is more or less unquestioningly adopted by modern scientists and its more precise rendition as a transference theory is the backbone of causal notions (if they are acknowledged at all) in physics. To be fair, among single theories, transference is quite powerful, but for understanding life, probably not powerful enough, at least not alone.
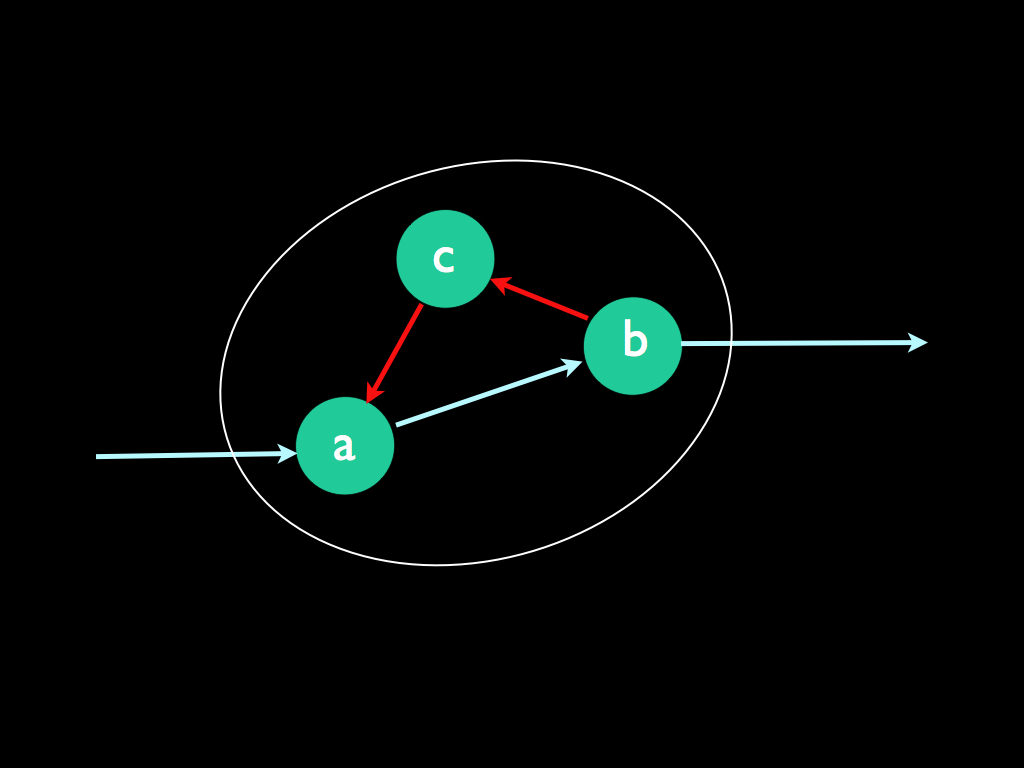
| Three kinds of efficient
cause. Here we have a familiar problem: the everyday language used to describe causation is not at all adequate to convey the variety of specific meanings that we need in order to understand the phenomenon. In particular, the single word 'cause' is insufficient to relay all the different senses in which A causes B, so we are often left to guess in the face of an ambiguous statement of that kind. Worse still, the common use of directed graphs (as in the diagram below) to convey ideas about causation also suffer from ambiguity because the arrows have to represent several senses of causation. How should we read this graph? 1. It might merely mean that a signal entering (a), passes to (b) and leaves, but is acted upon by (a) and (b) in such a way that includes the feedback path leading from (b) via (c), back to (a). In this case the system (a,b,c) is nothing more than a processor that includes feedback and cause is merely meant in the sense that the behaviour of (a,b,c) causes the signal transformation from input to output. 2. In a second reading, (a), (b) and (c) could represent states of a system X, which maybe can take any one of n states of which these are examples. In this case, which I will call 'state-constraint', we read the graph as: the system is put into state (a) by the input, this state transitions to state (b) which constrains the output and also causes a transition into state (c) from which the system must enter state (a). Alternatively, there might be three distinct system variables (a, b and c), which are dependent upon one another in the way described by the directed graph: (a) depends on the input, but the set of states it may take are constrained by the causal effect of (c), which is in turn constrained by that of (b), but (b) is constrained in the set of states it can take by the causal effect of (a). 3. Finally, a, b and c might represent particular concrete systems, the existence of which depends on one-another. In this ontological case, cause has the meaning of 'cause to come into existence' and (a) brings about the existence of (b) which in turn does this for (c) and in turn (c) brings (a) into existence. Here we have the most puzzling recursive loop of creation, which never the less, encapsulates the meaning of autopoiesis in biology. These different concepts of causation will be resolved and clarified when we come to consider Robert Rosen's approach to biology below.
|
Indeed, most of the formal work on causation deals only with efficient cause and most of that deals only with the second 'state-constraint' meaning of efficient cause (e.g. see manipulation theories below). However, to explain the essence of life and how it comes to exist at all, we need to take ontological causation seriously.
Ontological Causation - Robert Rosen's Relational Theory
In 'What does it take to make an organism?' (2000), the leading theoretical biologist Robert Rosen (1934-1998, pictured below) argued that science as a whole had got stuck with a hypothesis that can be traced back to Isac Newton and that it was so entrenched that most of us don't even notice its constraint on our work. This hypothesis is (in Rosen's words) that "epistemology entails ontology and particulars entail generalities [so that] particulars entail everything". By "epistemology entails ontology", he mean that we are led to assume that knowledge of what things are made of and how they work is entirely sufficient to explain how they came to be (ontology). By "particulars entail generalities", he meant that we are expected to derive our general understanding (e.g. of life) from studying particular cases of living organisms, or better still, the molecular details of them. The conclusion is that we look for an explanation of how life comes into existence and what it essentially is, by comprehensively studying biochemistry, genetics and biophysics (see this is exactly the physicalist position). For Rosen, this is misguided. He insists that ontology (specifically why life exists at all) is separate and not derivable from the mechanisms of functioning organisms. The problem seems a subtle one, but it has very profound consequences for the way we understand the essence of life. It is clearly one that has arisen by most scientists unconsciously adopting a physicalist view of causation, along with its limitations, of course, but because most scientists know no different, they are unaware of these limitations.

Rosen advocated the alternative (what he calls pre-Newtonian) position where ontology and epistemology are separately indepenendent, particularly because he believed ontology involves a different causal structure from that seen in epistemology: ontological causality cannot be explained in the same way or terms as that used for the observed processes and mechanisms of systems (i.e. physicalism). This is certainly not a matter of nostalgia: he was far sighted and open minded enough to realise that the fundamental question of why (e.g. living systems) exist, i.e. how they came into being in the physical world, was a question that had been neglected by science precisely because science had narrowed its philosophical basis to such an extent that it was incapable of even formulating the question.
He was inspired by the rather overlooked*, but brilliant theoretician Nicolas Rashevsky (1899-1972) who (as so many theoretical physicists have done - notably Schr÷dinger of course) embarked on a quest to explain life in terms of physics. By Rosen's (2000) posthumous account, Rashevsky found that the more detailed and foundational his mechanistic models became, somehow the further away they seemed from the 'essence' of life he was trying to capture. Faced with this, in a burst of creative thinking, he developed a new concept which he called relational biology. It is an approach that concentrates on the 'organisation' of organisms, rather than their material composition, so in a way it is one of the founding principles of this website's aim. By organsiation, we can think of information and control structures and can leave the matter aside because we know that systems described this way are multiply realisable. Rosen developed this idea (Rosen, 1983) into a useful theoretical construct which he called the (M,R) system, in which M stands for metabolism ("what goes on in the cytoplasm", which must include molecular assembly) and R stands for repair ("what goes on in the nucleus", meaning information maintenance). If this seems too abstract and naive (after all two of the three kingdoms of life don't even have the nucleus), it is because at this point Rosen is, like an artist just placing the first blocks of colour to define the overall shape of their painting, only thinking aloud the strategy for his theory. We can think of 'metabolism' as the processing architecture which physically enacts life and 'repair' as the systems which maintain its integrity (these in practice include an inherited - digital - store of information: the DNA and RNA often referred to as the 'blue prints'). The power of the (M,R) system, is in showing, with fundamental mathematical rigour, how a system can be the creator of itself.
* This despite the fact that he was one of the originators of the field of mathematical biology and responsible for many of the important developments in that field, long before some more famous people received credit for them.
(M-R) Systems and self-causation
We can start with the M sub-system as a 'black-box' with one input x and one output y : M transforms x->y, which is an act of state-constraint efficient cause on x that results from the configuration (embodied information) of M. This configuration is constantly vulnerable to decay (second law of thermodynamics), so to keep its integrity, it needs another sub-system that maintains it: R is such that its outputs are the components of M. Rosen proceeded using set theory, and a 'forensic' comparison of formalisms concerning causal representation (for which he deploys category theory), but we can summarise his use of it without being too technical here.
Usually, the (M-R) system is summarised in the following three relations (noting that A and B are sets of, e.g. biologically functional molecules within the cell with the role of inputs and outputs to the M subsystem respectively).
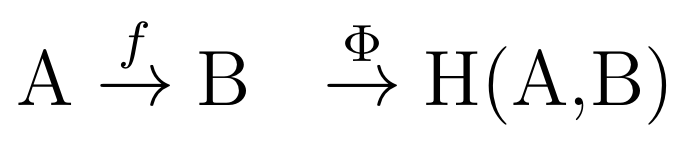 1
1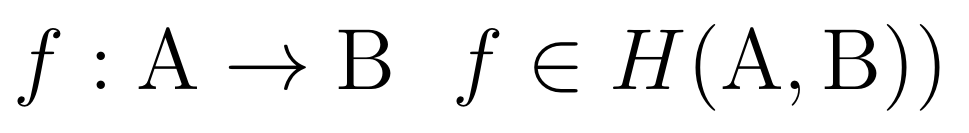 2
2 3
3These relations are expressed through mathematical mappings, which are a more general, fundamental and therefore powerful idea than mathematical functions (e.g. the familiar straight line in Cartesian coordinates x,y: y=m x +c is an example of the mapping X -> Y, in which X is a set (termed the domain in set theory) and Y is also a set (termed the range) and in this case both X and Y are the set of natural numbers. Sets can be of any kind of mathematical object that could be collected together by sharing a something in common. If the (M,R)-System represents a biological system (which is the intention), then the sets are collections of molecules or of molecular processes such as reactions, changes in conformations and so on).
The first relation (1) serves as a definition of the (M,R)-System, where a set of inputs A is transformed into outputs B under the system's action (represented mathematically as a mapping f). H is the set of all the mappings (the whole set of arrows in a directed graph), which represents the (causal) functions of the M-subsystem. In the case of relation 1 above, there is only one arrow (labeled f) and this is what Rosen termed the "metabolic processor". This is put formally in the second relation (2), which says that the mapping f is from a domain A to a range B and that f is an element (the only one so far) of H(A,B).
The R-subsystem is defined similarly as a mapping (Phi) from the M-system's outputs (B) to the set H of functional relations (the M-system itself). So the first relation (1) in total says that a network of processes (H(A,B)) is generated (via the mapping Phi) from a domain B, but that is itself generated by the processes H(A,B). In the third relation (3), we see that the R-subsystem (Phi) is itself a member of the set of processes H, but this time, mapping not from A, but from B, to produce H(A,B). In other words, the same set of processes both produces B (when acting on A) and also, when acting on B, it produces itself!
Now it might be intuitive, but certainly with some careful mathematical analysis, it has been proved that this definition is an abstract generalisation of autopoiesis and that all autopoietic systems are examples of (M,R) systems (see Zaretzky and Letelier, 2002, where this is demonstrated). In sections 10.C and 10.D of Rosen (1983), he makes it clear that he already understood this to be the case, but before we get there, we have to add one more crucial elaboration of the (M,R)-System: reproduction.
Already, we see that a powerful feature of these set-theory relations, I shall call them Rosen's relations, is that they formalise the way in which it is possible for a functional system to be the cause of itself. To help understand this and work with these sort of relational systems, Rosen gave us relational diagrams (below), which he terms abstract block diagrams. First, to define the symbols, the simple mapping:
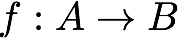
(which is the first step in Rosen relation 1 above) is represented with diagram 1 (below), where a hollow headed arrow denotes flow from input A to output B, which is associated with Aristotle's material cause and the solid headed arrow from f to A denotes the generation of this flow by the processor which is associated with Aristotle's efficient cause. As we saw, in his relational theory, cause and effect are more precisely and comprehensively understood through mappings on sets, where the mapping is itself an entailment, meaning that if the set A maps to the set B, then for any element a that is a member of A, there exists some element b, which is thereby necessitated by both a being in the domain A and the mapping f itself. Here we have a separation of necessary conditions a and f. Rosen identifies them as the sources of different kinds of entailment, which implies they are sources of different kinds of causation.
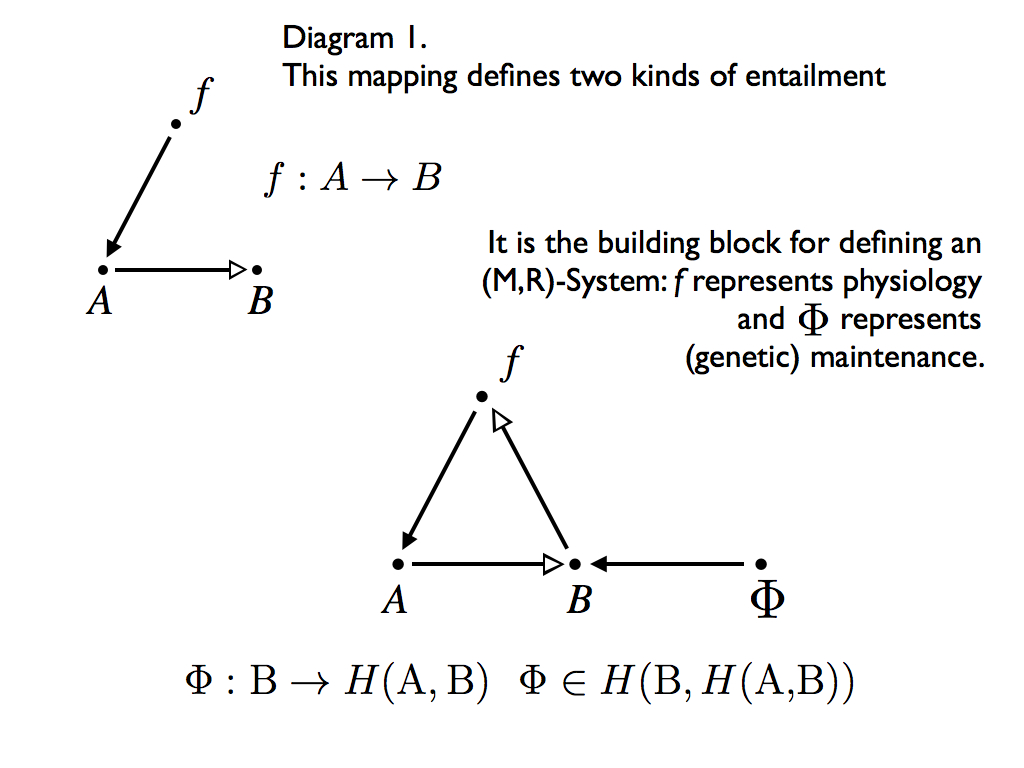
The second diagram (now above) is the definition of an (M,R)-System in the form of an abstract block diagram (with the set theory definition written below it). Notice how the R-subsystem, represented by Phi, is the (efficient cause) entailment of B and in that way it becomes the (material cause) entailment of f. In other words, Phi uses B to make f. Well, you might have thought there was something 'fishy' about this when you saw it expressed in set-theory as relation (3) above. Why is B the raw material for making f ? All I can do is quote Rosen verbatim (p249 from Rosen 1983) and assure you that he was forensically careful in constructing his arguments. Referring to diagram 1, he says:
"In such a diagram, the processor f is itself unentailed. As we saw, one way to entail it is to enlarge the diagram , to throw in a new processor Phi, a new mapping, which intuitively makes f from an appropriate set of inputs X. For maximum economy, we may take X=B; Why not?"
That's it. Rosen avoids an infinite regress of mappings making mappings making mappings by simply letting the source for making the original mapping processor the material produced by it. The economy he refers to is three-fold. First it saves a lot of trouble drawing a bigger and bigger diagram, second, it cuts off the infinite regress (so efficiently solves a logic problem) and third, the use of products in making the the thing that produced those products is precisely the economy deployed by nature in organisms. However, we now see that Phi itself is stuck out on a limb without anything to entail it, as Rosen puts it "we do not have enough entailment in the system to answer the question 'why Phi?' ", so we are not out of these woods yet. In response, Rosen invokes a third function for the system: that of replication. You can imagine this as an additional pair of arrows representing the replication (he labels it beta) making Phi out of B (and thereby incorporating a second 'economy'), but that would only demand the same for beta and so on... another infinite regress. Of course, Rosen has a much better idea. He shows that the replication function is already entailed in the (M,R)-system (relation (3) above). His argument for this is only briefly sketched in Rosen (1983), but more fully explained in his earlier work. The result is the diagram below which contains two more entailments. Crucially an element of B is used as a function to make Phi via f, but the argument is more complicated than just adding this. It turns out that the element of B has to be the inverse of beta for this to work.
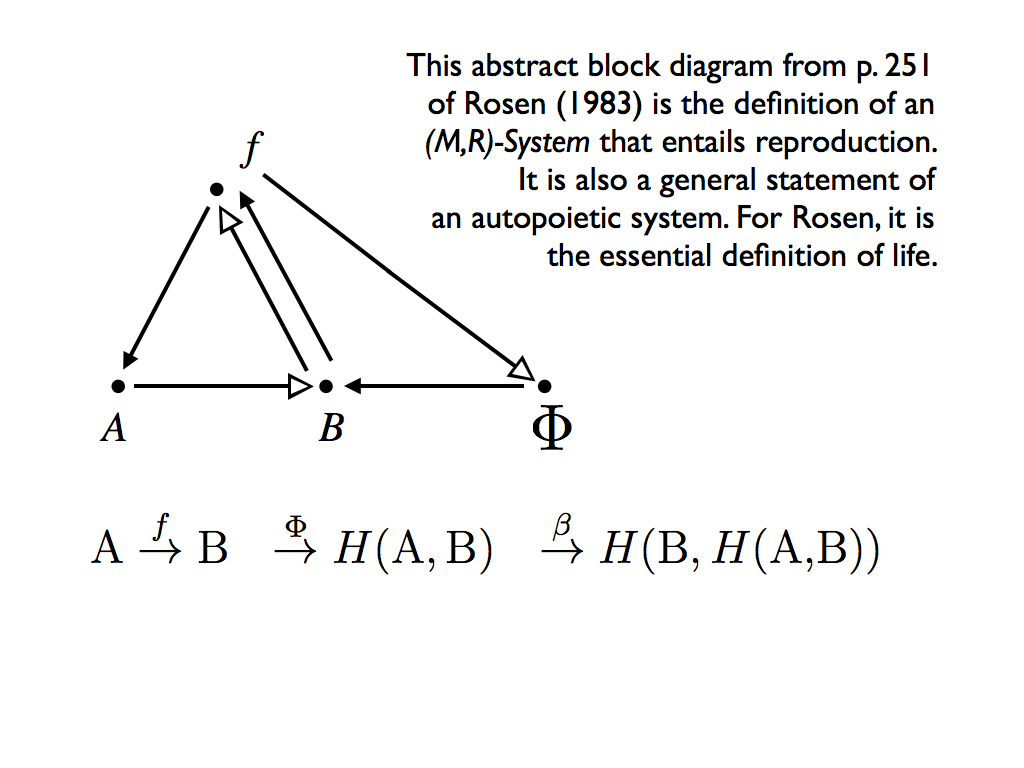
This diagram is his masterpiece. It shows an abstract system entailing itself, embodying both efficient and material causes to reflexively answer the "why?" question of ultimate cause. This is effectively the same thing as saying the system is closed to efficient cause. Significantly Rosen uses that in his definition of an organism: "A material system is an organism if and only if it is closed to efficient cause". Then the (M,R)-System is a relational model of a living organism that captures this necessary and sufficient condition: the replication function given in the last abstract block diagram is entailed, in the sense of efficient cause, entirely in the definition of an (M,R)-System (relation (3) above).
"...everything in it is entailed in the sense of efficient cause entirely within the diagram. Any material system possessing such a graph as a relational model (i.e., which realizes that graph) is accordingly an organism."
Clearly Rosen's work, although rather abstract at this point, is something very important to our progress in understanding causation as it relates to what life actually is, rather than merely how it is implemented in material (the stuff that biologists are mainly concerned with).
Cause as entailment
The separation of material and efficient cause, more precisely put as a resolution of different kinds of entailment is crucial in Rosen's relational theory. He does not dismiss ultimate cause as scientists are strongly encouraged to do. He recognises that ultimate cause is not banished by the machine metaphor that has so strongly pervaded science since Newton, rather it has been highlighted by it, since the parts of a machine, being each designed for a particular role within it and therefore being functional must thereby have a purpose. This is especially embarrassing for biologists who have to contend with the persistent efforts of creationists. The standard repost is that natural selection has evolved design and function is no more than the appearance of suitability that was selected by competitive replication. Rosen sees through this thin argument: evolution is a phenomenon of life, not the other way around. He proposes a much more logically grounded and stable answer. It is that life is specifically a system with sufficient entailment that it becomes the efficient cause of itself. The way he did this, working with category theory on set theory means that his idea is more general and deeper than that of autopoiesis. However, it remains rather neglected because the cost of this great generality and mathematical strength is that it has proved much too abstract to influence the majority of biologists. The challenge, for those that believe in Rosen's accomplishment, is to interpret the (M,R)-System in terms that are practically meaningful for mainstream biological problems. (see circular causation and autopoiesis).
Cause as Constraint
For Rosen, efficient cause is a form of entailment: X entails Y meaning that Y necessarily follows from X. This has several subtle connotations, one of immediate practical use being that of constraint: X constrains Y to be what it is. This interpretation was central to MontÚvil and Mossio's (2015) theory of "biological determination as self-constraint", by which they meant that the self-determination of living organisms is a result of self-causation, which in turn results from the constraint of internal processes by internal configuration. Self-determination here means constitutional autonomy, which is both an interpretation of autopoiesis and an implication of autonomous agency. You will note that constraint is a useful idea because it leads directly into information (recalling information is defined in relation to entropy as a constraint on configurations). Indeed this constraint interpretation of cause may, with some further work, enable the quantification of cause.
But MontÚvil and Mossio's (2015) have a weaker kind of causation in mind than Rosen seemed to have. They refer to 'influence', not the 'fabrication' of components explained by the self-replicating (M,R)-System, but the determination of processes (the efficient cause emanating from f in an (M,R)-System), especially through the action of catalysis. Like Rosen, these authors distinguish between 'process causation' (at least roughly equivalent to material cause and referred to as 'flow' - the hollow arrows - by Rosen) and 'constraint causation', which (confusingly) is equivalent to Rosen's processing - solid arrows - and roughly equates to Aristotle's efficient cause). It becomes a little clearer in mathematical notation:
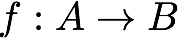
where f is a constraint, following MontÚvil and Mossio's (2015) definition:
f is a constraint if and only if i) some physical quantity (e.g. energy) is not conserved at some specific (characteristic) timescale t with respect to B, and ii) with respect to f , there is always a temporal symmetry (conservation of the same physical quantity). Symmetry, so defined as the conservation of a physical quantity, or less precisely but in more familiar terms, invariance as in whatever enacts f is unaffected by doing so, is an essential part of this definition. So, and most unlike Rosen, is the explicit timescale (acknowledging that the material and configurations responsible are all ultimately ephemeral). More concretely (but less generally) this is effectively a description of catalysis: f influences the transformation of A to B, without itself being changed. Thus, for MontÚvil and Mossio (2015), efficient cause is enacted as a generalisation of catalysis, at a characteristic timescale and considered to be an influence on the material transformation from A to B.
Using this elemental building block, they build up hypothetical networks of time-specified causal influence, a simple example of which is shown below (taken from their paper).
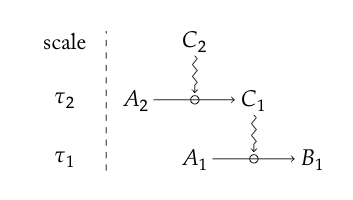
The key differences between their constraint interpretation and that of Rosen are well depicted here - the explicit timescales of action and the squiggly lines indicating influence, rather than the solid headed arrows of Rosen's transformative cause. We can also see where this is going because there is the potential to interpret 'real-life' realisations (biomolecular pathways) with a diagram of this sort and thereby identify the causal structure of a living system: in other words to make Rosen's concepts more concrete. In fact, MontÚvil and Mossio (2015) went a lot further than that. They placed hypothetical networks of constrained processes (as the simple cascade above shows) in the context of "closure to constraint" to show the sort of organisational closure that appears in Kauffman's autocatalytic sets that were formally analysed as such by Hordijk and Steel (2004). Indeed their definition of closure is essentially the same as that used by Hordijk and Steel (2004), except it refers, more generally, to constraints:
A set of constraints C realises overall closure if, for each constraint C_i belonging to C:
1. C_i depends directly on at least one other constraint belonging to C (C_i is dependent);
2. There is at least one other constraint C_j belonging to C which depends on C_i (C_i is generative);
A set C which realises overall closure also realises strict closure of it meets the following additional condition:
3. C cannot be split into two closed sets.
1. C_i depends directly on at least one other constraint belonging to C (C_i is dependent);
2. There is at least one other constraint C_j belonging to C which depends on C_i (C_i is generative);
A set C which realises overall closure also realises strict closure of it meets the following additional condition:
3. C cannot be split into two closed sets.
We note the relational categories dependent and generative in this definition. Dependence has a specific meaning for MontÚvil and Mossio (2015), which is strongly related to the R side of Rosen's (M,R)-system. They say:
"...constraints are defined as entities which, at specific time scales, are conserved (symmetric) with respect to the process, and are therefore not the locus of a transfer. However, constraints are typically subject to degradation at longer time scales, and must be replaced or repaired. When the replacement or repair of a constraint depends (also) on the action of another constraint, a relationship of dependence is established between the two."
More precisely, they give the following definition:
1. C_1 is a constraint at scale t_1,
2. There is an object C_2 which at scale t_2 is a constraint on a process producing aspects of C_1 which are relevant for its role as a constraint at scale t_1 (i.e. they would not appear without this process). In this situation, we say that C_1 is dependent on C_2, and that C_2 is generative for C_1.
2. There is an object C_2 which at scale t_2 is a constraint on a process producing aspects of C_1 which are relevant for its role as a constraint at scale t_1 (i.e. they would not appear without this process). In this situation, we say that C_1 is dependent on C_2, and that C_2 is generative for C_1.
By now, this is familiar from Rosen's idea of 'maintenance', but includes an explicit account of the different timescales over which processes and their maintenance occur. It could also be concluded that a set of constraints that realises strict closure amounts to an (M,R)-System. MontÚvil and Mossio (2015) put it this way: "What matters for our present purposes is that closure, and therefore self-determination, is located at the level of efficient causes: what constitutes the organisation is the set of efficient causes subject to closure, and its maintenance (and stability) is the maintenance of the closed network of efficient causes."
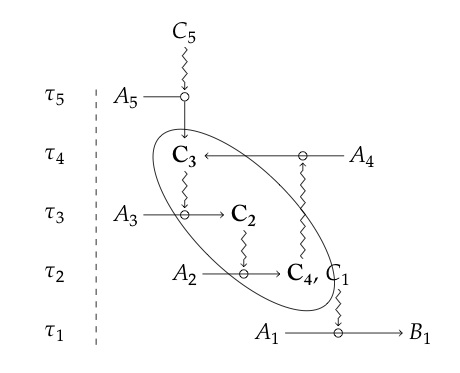
We can summarise their ideas with their illustrative diagram (above). Here, C_1 to C_5 are, by their definition, constraints with t_1 to t_5 the characteristic timescales of each. C_1 to C_4 are dependent constraints and C_2 to C_5 are generative (so C_2 to C_4 are both). These three (circled in the diagram) are organised to realise strict closure in terms of constraints because C_4 is generative for C_3. There is obviously a relationship between this diagram and the previous Rosen relational diagram for an (M,R)-System; though it is nothing like as general, it does have the advantage of explicitly accounting for timescales. It was intended only to illustrate their points, but it has to be admitted that like this, it does not carry the deep meaning of Rosen's system. That is because here there is not in-principle reason for arranging the constraints so as to realise closure, whereas Rosen explicitly provided the reason. All the same, we can see that ontological cause, which is an account of how things come to be (self-generated) consists of material causes (processed for MontÚvil and Mossio (2015)) under the generative effect of constraints (efficient causes) if they are organised to realise closure. Ultimately it is this organisation that enables the ontological cause to be formed: one of Rosen's important contributions was to show that this is both necessary and sufficient. It could be said that this is an example of the role of Aristotle's formal cause (see definitions above). The hunt is now on for structures like this in real biological (e.g. molecular or ecological) networks.
Causal language for biology - a summary so far
We have met several different kinds of cause so far, but, in the terminology of Aristotle, most of the talk has been about different kinds of efficient cause, with acknowledgment of material cause and a brief mention, just now of formal cause. We have not used ultimate cause, though it is there in the background for those that are not too inhibited by current scientific convention to admit its possibility. In Rosen's work, we saw cause interpreted as entailment (making something necessarily follow if the cause is present). In MontÚvil and Mossio (2015), we saw it interpreted as constraint and, for ourselves, noted the closeness of this idea to that of information as defined by entropy. Constraint seems both more general and more specific than the processing (efficient) cause of Rosen's solid-headed arrows. There is entailment, but it is partial, since influence does not imply absolute determination. This is far closer to the idea of information instantiated in a configuration constraining the option space for the system which embodies it. We can interpret both efficient cause and formal cause of this constraining kind in every day language (though realising that it is therefore not going to be sufficiently precise to do the proper work of science with). That is exactly what I did when introducing causal power as a preamble to explaining downward causation (based on Farnsworth et al., 2017). Here it is again:
"Causal power is attributed to an agency which can influence a system to change outcomes, but does not necessarily itself bring about a physical change by direct interaction with it. In an easily grasped analogy, the Mafia boss says his rival must be permanently dealt with (the boss has causal power), but his henchman does the dirty deed. The action of the henchman is physical and dynamic and the henchman is logically described at the same ontological level as his victim (it is not the cartel that kills the rival, not the rotten society, not the atoms in the henchman’s body, but the henchman himself). A dynamic, physical cause linking agents of the same ontological level is referred to as an effective cause (alternatively efficient cause, following Aristotle (Falcon 2015). So, when a snooker ball strikes another it causes it to move, and that is an effective cause. But the laws of physics that dictate what will happen when one ball hits another are not effective causes, even though they do have causal power (as such they are called formal causes). It seems that effective cause is always accompanied by a transfer of energy: this is the only way in which a physical change can take place in the physical universe. However, for an effective cause to be realised, non-effective causes must also exercise their power".
In this case, we might interpret these non-effective, yet powerful causes as the 'catalytic' constraints of MontÚvil and Mossio (2015) because they are conserved and yet have an influence on the behaviour of the system. That would get some of it, but not all. The reason is, of course, that the configuration (in this case the network or interacting constraints) matters as well and that (formal cause) is also conserved, yet powerful. In the transference (physical) theory of cause, some physical quantity like energy or momentum is transferred to enact the cause, but this occurs under the influence (constraint) of a non-effective, yet powerful cause that might well be a configuration (i.e. formal cause), which can only be identified as information (see the entropy page to understand why). This link with information was not explicitly identified by either Rosen or MontÚvil and Mossio (2015), though it is given a nod of acknowledgment by some other authors on the topic.
The search for cause
After all that theory, we now turn to the question of how causation can be studied empirically. It turns out that identifying cause, let alone quantifying it, is much more complicated and challenging that a naive glance would suggest. The slide below summarises the methods so far available to detect and quantify causality: all of them have severe limitations or drawbacks.

The first three are all closely related statistical approaches cast in terms of information theory and clearly in the David Hume tradition of empiricism. Most readers will be familiar with correlation (a statistical measure of how much one variable depends on another) and the generalisation of this through information theory, which is of course 'mutual information' (see Adami, 2004 for a good introduction to this sort of thing). In all three, we are looking for causality in time-series data that represents the behaviour of a system (or components of it) through variable attributes. This limits the scope to state-constraint efficient cause (as I define it in the box above). They are also limited to temporally linear systems (what Rosen (1991)terms 'chronicles'), so are not at all capable of analysing the circular causation that is so important in understanding biological systems. But we have to start somewhere and this is it. By definition a variable x: [x(1), x(2) ... x(t)] has Granger causality on y (another time-series) if including it predicts y(t+n) better than without it (i.e. from autocorrelation on y). This is conceptually equivalent to saying that cause is revealed by predictability, or more precisely, by mutual information (which is manifest in cross correlation). Shreiber's Transfer Entropy is just another way to calculate this.
Modular Response Analysis is an application of the concept used for the more general structured equation modeling (SEM), designed specifically for studying molecular networks (hence its relevance here). SEM is an entirely statistical approach, again using correlations, to quantify the strengths of mutual influence (or constraint) among a set of variables, which might for example represent the state of individual components (e.g. molecules) in a system. Assigning causality to the relationships among the variables is a common mistake: it is wholly unjustified in SEM. This is because SEM cannot discern the direction of causation: the results are symmetrical.
It seems the available quantitative methods, based on mutual information among time-series variables are a disappointing avenue of inquiry for our purpose. The only known alternative involves some kind of perturbation analysis, or what in the philosophy of causation has been termed 'manipulation'.
Manipulation Theories
According to mainstream modern philosophy, currently, the most powerful means by which we may identify efficient causation is via manipulation, underpinned by ‘manipulability theories’ (Woodward, 2016). Among these, the most supportive of modern scientific thinking is the ‘interventionist’ approach formalised (and popularised) by Pearl (2009) and also, in a better founded equivalent by Woodward (2003) and Woodward & Hitchcock (2003)*.
* Pearl's approach is far better known that Woodward's, other than in professional philosophy circles, perhaps because there remains a rift between science and philosophy. Pearl is essentially a statistician / computer scientist; his approach is more accessible to other such professionals, but Woodward's is more careful to avoid hypothetical paradoxes, so is more robust to philosophical scrutiny. Also Pearl seems to be an able and enthusiastic publicist for his work.
Manipulation is a simple idea and rather obvious to anyone who tries to locate a problem in, e.g. a faulty machine or debug a computer program. If a car mechanic does not recognise a fault immediately, then their ususal strategy will be to adopt a 'process of elimination' to identify the cause. This amounts to removing or isolating different parts until there is a change in the sysmptoms. That is what manipulation means in this context. It is really a contrast with the non-interventionist approach of observing the behaviour of the system and deducing causal connections from the results. The point is, getting active and manipulating the system is more effective than just observing it - manipulability theories formalise the method (especially through statistical analysis) and its basis.
The interventionist approach conceives of efficient causal relationships represented as directed graphs which summarise the effect of one `variable' on another, summarising the dependencies in a system of equations that relate all the relevant variables to one another (the connection to structured equation modeling in statistics is not accidental). This means that manipulation theories only deal with a narrow concept of causation (the state constraint kind - see box above). Note that the consideration of the states of components in a system (states represented as variables) X, Y, etc.), rather than their very existence, means that manipulation theories do not (obviously) apply to self-assembly. Manipulation theories are conceived only in relation to state-dependent systems.The interventionist approach simply sets up a test for e.g. X causes Y by intervening to change X from x to x’ and observing what happens to Y that is different if the manipulation had not been conducted. This is posed as a ‘mind experiment’ in terms of a counter factual: If X were manipulated something would happen to Y.
Pearl’s formulation seems (superficially) to be one of the foundations for Integrated Information Theory (IIT) (laid out in Oizumi et al. 2014). Pearl terms the equations of the system as ‘causal mechanisms’ and the intervention appears as a setting of a single mechanism, without altering any of the others (implying the assumption that mechanisms are each autonomous in the mathematical sense). This is both the basic approach and the language of IIT (see for example Marshall et al., 2017). On the other hand, the analysis of IIT in relation to intervention by Baxendale and Mindt (2018) very much implies that the authors of IIT had a different framework in mind: one much more closely associated wth information and its interpretation in psychology.
IIT is of particular interest to us here because it is intended to reveal and quantify the internal causal structure of a system (as part of a method to quantify a particular notion of consciousness attributed to Giulio Tononi (2004), who first conceived IIT*).
* The date here may suggest Tononi was first, with Pearl following his lead, but Pearl's book summarises work published over at least ten previous years of study, mainly in structured equation modelling.
Having been convinced by Woodward’s arguments, I will continue with his formulation, which starts as follows (from Woodward (2016):
...an intervention V on a variable X is always defined with respect to a second variable Y (the intent being to use the notion of an intervention on X with respect to Y to characterize what it is for X to cause Y). Such an intervention V must meet the following requirements (M1 - M4):
- M1. V must be the only cause of X; i.e., as with Pearl, the intervention must completely disrupt the causal relationship between X and its previous causes so that the value of X is set entirely by V;
- M2. V must not directly cause Y via a route that does not go through X ;
- M3. V should not itself be caused by any cause that affects Y via a route that does not go through X;
- M4. V leaves the values taken by any causes of Y except those that are on the directed path from V to X to Y (should this exist) unchanged.
Woodward and colleagues recognise that a state variable Y on which X has causal influence may also be under the influence of other causal and also random effects, so the isolated intervention has to be a manipulation of X from x to x’, in the context of a particular `background' B_i of influences. They formulate causation as a difference:
Y(x) | B_i - Y(x’) | B_i ,
and random (added noise) influences are accommodated by working in expectations: E(Y(x)) etc..
Circularity of argument is serious problem with interventionist accounts of causality (Woodward,2016), which can be overcome by the (Woodward, 2003) approach, at least in the instrumental sense of being able to identify a causal relationship without having to assume it first (which seems to be a problem with Pearl's (2009) approach). Woodward maintains that all interventionist accounts are circular and thereby incapable of escaping causal ‘talk’: it is not possible, with them, to derive causality from some more basic and independent notion: i.e. they are non-reductive.
Note: an alternative framework is that of causal process theory (Salmon,1984; Dowe,2000) which is that there must be a spatio-temporally continuous connection between X and Y involving the transfer of energy, momentum (or other conserved quantity) for X to cause Y. This is an example of a `transference' theory of causation.
Causal Closure - this to be updated and reformatted.
Organisational
and Causal Closure
This box explains the (at
first rather opaque) idea of closure and its different kinds. |
References
Adami, C. (2004). Information theory in molecular biology. Physics of Life Reviews. 1: 3-22.
Bertschinger, N.; Olbrich, E.; ay, N.; Jost, J. Information and closure in systems theory. German Workshop on Artificial Life <7, Jena, July 26 - 28, 2006>: Explorations in the complexity of possible life, 9-19 (2006), 2006.
Bertschinger, N.; Olbrich, E.; ay, N.; Jost, J. Autonomy: An information theoretic perspective. Bio Systems 2008, 91, 331–45.
Mossio, M.; Bich, L.; Moreno, A. Emergence, closure and inter-level causation in biological systems. Erkenntnis 2013, 78, 153–178.
Clark, A. (1997). Being There: Putting Brain, Body, and World Together Again. MIT Press, Cambridge (MA), USA..
Dowe, P. (2000). Physical Causation, Cambridge. Cambridge University Press, Cambridge, U.K..
Farnsworth, K.D. Can a robot have free will? Entropy 2017.
Farnsworth, K.D.; Ellis, G.F.; Jaeger, L. (2017). Living through Downward Causation. In From Matter to Life: Information and Causality; Walker, S.; Davies, P.; Ellis, G., Eds.; Cambridge University Press. Chapter 13, pp. 303–333.
Heylighen, F. Relational Closure: a mathematical concept for distinction-making and complexity analysis. Cybernetics and Systems 1990, 90, 335–342.
Hitchcock, C. (2018). Probabilistic causation. In Edward N. Zalta, editor, The Stanford Encyclopedia of Philosophy. https://plato.stanford.edu/archives/fall2018/entries/causation–probabilistic/. Meta- physics Research Lab, Stanford University.
D. Hume. (1748). An Enquiry Concerning Human Understanding. Oxford University Press, 2007.
Marshall, W.; Kim, H.; Walker, S.; Tononi, G.; Albantakis, L. How causal analysis can reveal autonomy in models of biological systems. Philos. Trans. R. Soc. A-Math. Phys. Eng. Sci. 2017, 375.
MontÚvil, M. and Mossio, M. (2015). Biological organisation as closure of constraints. J. Theor. Biol., 372:179–191, 2015.
Pearl, J. (2009). Causality. Cambridge University Press, New York, USA..
Rosen, R. (1991). Life itself: A comprehensive enquiry into the nature, origin and fabrication of
life. Columbia University Press, New York, USA..
Rosen, R. (2000). Essays on Life Itself. Columbia University Press.
Salmon, W. C.(1984). Scientific Explanation and the Causal Structure of the World. Princeton
University Press, Princeton, USA..
Varela, F.; Maturana, H.; Uribe, R. Autopoiesis: the organization of living systems, its characterization and a model. Curr. Mod. Biol. 1974, 5, 187–96.
Vernon, D.; Lowe, R.; Thill, S.; Ziemke, T. Embodied cognition and circular causality: on the role of constitutive autonomy in the reciprocal coupling of perception and action. Frontiers in psychology 2015, 6.
Woodward, J. (2003a). Making Things Happen: A Theory of Causal Explanation. Oxford University Press, Oxford, UK.
Woodward, J. (2003b). Explanatory generalizations, part i: A counterfactual account. Noűs, 37(1):1–24, doi:10.1111/1468-0068.00426 2003b.
Woodward, J. (2016). Causation and manipulability. In Edward N. Zalta, ed- itor, The Stanford Encyclopedia of Philosophy (Winter 2016 Edition). https://plato.stanford.edu/archives/win2016/entries/causation–mani. Metaphysics Re- search Lab, Stanford University.
Zaretzky A.N. and Letelier J.C. (2002). Metabolic Networks from ( M,R ) Systems and Autopoiesis Perspective. Journal of Biological Systems. 10 265-284.
see also (further reading):
Hordijk, W.; Steel, M. (2004). Detecting autocatalytic, self-sustaining sets in chemical reaction systems. J. Theor. Biol. 227, 451–461.
Kauffman, S.A. (1986). Autocatalytic sets of proteins. J. Theor. Biol. 119, 1–24.
Kauffman, S.A. (1993). Origins of Order: Self-Organization and Selection in Evolution; Oxford University Press: Oxford, UK.
Kauffman, S.A. (2000). Investigations; Oxford University Press.
Mumford, S. and Anjum, R. L. (2013). Causation A very short introduction. Oxford University Press.
Oizumi, M.; Albantakis, L.; Tononi, G. (2014). From the Phenomenology to the Mechanisms of Consciousness: Integrated Information Theory 3.0. PLoS Comput. Biol. 10.
Tononi, G. (2004). An informational integration theory of consciousness. BMC Neuroscience. 5, 42.