Circular Causation

  Under construction 26-02-20: I have started to develop this page a bit more.

  Here I provide a brief introduction to the issue of circular causation of the form A->B->A,
(-> representing 'causes'), which is, on the face of it, impossible because it violates the order of precedence (efficient cause must preceed its effect). It also seems impossible intuitively because it obviously means something being the cause of itself. It is important here because circular causation lies behind major ideas such as autopoiesis and the very essence of life (in the sense of Robert Rosen's work). Does that mean these ideas are nonsense? Certainly not: the problem is with particular habitual and largely unrecognised constraints on the way we think about processes. Here we aim to break free of those constraints and understand circular causation sufficiently to appreciate what is probably the deepest and most essential characteristic of life itself. We recommend you read the pages on Causation and Emergence before this one.

First, to summarise our position on causation.
1) All efficient cause entails and results from physical force (one of nuclear (strong and weak), electrical (with magnetism) and gravity (though from general relativity, that is not properly a force)).
2) Physical forces all cause (or prevent) movement and have a direction in space. The realised movement is the vector sum of all the physical forces acting on a particle at one time.
3) In the absence of constraints, the vector sum of forces acting on each member of an assembly of particles is random (because forces can act in any direction).
4) Constraints reduce the range of directions of action of forces among an assembly of particles.
5. Constraints always result from the relative position of particles in space.
6. The relative positions of particles and hence the constraints embody information as form (see Information Theory).
7. Form is both the embodiment of information and the information which organises the particles into a particular configuration.
8. The constraint of efficient cause by form is formative cause, which is my preferred definition of formal cause.
9. Underlying material cause, we also find the (atomic level) constraint by form of efficient cause. In this sense, material cause can be regarded as micro formal cause.
10. When an assembly of components is formed such that it performs autopoiesis with self-replication (constitutive circular causation), then it embodies ultimate cause. No other source of ultimate cause is known (with the implication that ultimate cause is uniquely a property of life). The reason is that ultimate cause necessarily implies a purpose and purpose is a property that only an autopoietic system can possess: the explanation can be found in Rosen’s argument on the ontological question (“why this system?”). Constitutive circular causation is the process of a system making itself and its purpose is simply to do so: it is constituted in such a way that it will.

Note that using this way of thinking about cause, the four (Aristotean) causes are systematically linked and also, since at the root all of them arise from the constraint of physical forces and constraint is identified with information, there is the means of quantifying all of them, via the quantification of information. Note also the relationship between this formative information and the concept of function.

Causation as constraint and the problem of time-order solved by information bootstrapping.

The conventional view is that A->B->C->A is impossible because causation must respect time-ordering. However, if we (more precisely) interpret cause as constraint, which is the information specifying the degrees of freedom for an assembly  of particles, then A->B->C->A means the information embodied in A constrains the assembly B .... which constrains the assembly A. This reduces the conundrum to the question: "how can A constrain itself". Let us label as A', the information that constrains (and therefore forms) an assembly of components (the material particles) into the object A. That is, A' arranges the particles into a particular form which is what we call the material object A.  The form of A interacts with that of B, which more deeply means that A' constrains B'. In other words, we are really looking at a purely informational phenomenon in which one arrangement of particles interacts with another in a way that constrains the arrangement options for the second. An obvious biological example of this sort of thing is the constraint by messenger RNA applied to the matching location of a transfer RNA. In information terms, the constraint is just an operation of information processing: that of maximising mutual information (and it is a very common and basic one). Note, it is not necessarily the whole assembly of the two interacting forms that match - which would result in replication - it can be, and usually is, just one part of them; the rest being constrained internally, or by additional forms. Given this idea of constraint, there is no reason in principle why C' should not constrain A' by maximising mutual information with some part of it. We already know intuitively that the closed cycle of constraints that would be produced by this (A->B->C->A) is how a cell maintains itself: DNA is synthesised by proteins and RNA, which in turn are synthesised by others in a way that is constrained by DNA. The synthesised DNA is the same form as the constraining DNA, but it is not materially the same: it is an assembly of different atoms. For this reason, the cell does not have to violate the ordering of time, or perform any other physical paradox, because all the constriants are actually just interactions among bits of information.

So what we have just done is realise that A->B->C->A does not have to imply that A is the cause of itself in a material sense, it more likely means that the information A' that forms A is the cause of more information A' that can form more A. Replication is one thing, but this still does not get at the deep meaning of a thing being the cause of literally itself, rather than another copy.  The  answer to this is the idea of information bootstrapping. The forms A...C, when broght together, make an aggregate information system that, through the mutual constraints of its components, adds system-level (constraining) information. This system level information imposes addtional constraint on each of the component forms and arised from at least one of, and potentially all of, their interactions. In this way it is inevitable that when any one form, A, becomes part of such a system, it thereby takes part in the constraint - and therfore the formational refinement - of itself. Starting with a set of basic forms, whose only necessary property is that they interact in ways that constrain one another into more precisely constraining forms, a process of information bootstrapping will ensue.



Closure
Connected with the concept of circularity is that of closure (loops are definitively closed: an open loop is no longer a loop).

At its most fundamental, closure is a mathematical concept applying to sets and operations. In general, a set ‘has closure under an operation’ if performance of that operation on members of the set always produces a member of that same set: this is the general definition of operational closure. If the operation is relational (e.g. A>B), then the system has relational closure if it has operational closure under the relational operator (note then that no finite system can have relational closure under the 'greater than' operator '>', but it could have under an operator such as 'connected to', e.g. A is connected to B is connected to A). More abstractly (but powerfully), mathematicians will say that the set of real numbers is closed to addition because the relational operation A + B, where A and B are both real numbers always produces another real number. In this sense closure implies that one cannot get out of the set, no matter how devious and complicated one chooses combinations of the operation. The set of real numbers is obviously not closed under the operation of taking the square root, since negative numbers are real and the square root of them is not (it is equivalent to multiplying by i (the square root of -1)), so the outcome takes one out of the set.

A chemical example
The most relevant example here is not really mathematical, it is descriptive of chemical reactions. Let R be a set of possible chemical reactions and X be a set of possible chemicals (molecules). This system has relational closure to R only if every reaction in R, acting on any combination of members of X, produces (products) that belong to the set X.

Let's pause for a moment to consider the causality in this. Reactions change reactants (destroying them) and create the product. That is efficient causation. The reactants need to be the right kind of chemicals for the efficient causation to work: that is material causation. But underlying this, we know that electrons 'orbiting' in the chemical's atoms are interacting via the electrical force in ways that are constrained by quantum mechanical rules: that is formal cause.

At first sight, this does not necessarily imply any loops of chemical reactions, but it does not rule them out. For example, if X=(A,B,C) and R is restricted to ligation and cleavage (joining and splitting), then we could have A + B -> AB, but for the closure to be true, AB must be C (products must be in X). Because A + C ->B + 2A is also in R (it is the cleavage of C), we can have A + B ->C and A + C-> B + A + A, then A + B ->C, and so on in a perpetual loop of making and breaking C. Not very useful, but it is an illustration (and something rather like this goes on in the ozone layer).

The property of closure is not necessary for loops to form: the little loop described above may be one of the reactions from a larger non-closed set involving, say, A + D -> AD and AD + B -> AE + AF, none of which are in the loop. You will notice that the last reaction removes B from the system, effectively killing off the loop anyway.




The set X=(A,B,C,D,E,F,AB,AC,AD,AE,AF) is closed to the reactions R=(A+B ->AB,  A+C ->AC,  A+D->AD,  AD+B->AE+AF, A+AE ->E+2A, A+AF->F+2A). It is reasonable that these are the only chemically possible reactions, though there are many other hypothetical ligations and cleavages.  You will notice that every reaction in R produces a member of X (since I included all the products there). But also notice that not every member of X is a reactant (specifically, AB and AC are left as only products).  However, if we add two more restrictions, then we will find that loops are inevitable.

The first restriction is that the set X be finite. The second is that every product of a reaction in R must be a reactant, thus defining X as only those chemicals that undergo reactions in R. Then,  every reaction must produce a chemical that will also react with another member of the finite set X. The product of that reaction must also be a member of X. As long as the set X is finite (and all the reactants are available), then all chains of reactions must eventually produce at least one chemical that takes part in the chain. In fact, this more restrictive definition of X (a finite set of all available chemicals that take part as reactants in R) is closer to the mathematical definition of closure than what we started with. The mathematical definition supposed that the operation can be performed on all members of X: they must be available for operating on and at least one of the kinds of the operation must work on every one of them.  If no kind of R would work on say, A, then what is A doing in X? That would be like having the real numbers and a bannana in the same set - you could do addition or subtraction on all the numbers, but never on the bannana, so closure just doesn't make sense with such a silly set. All the real numbers are available for adding and subtracting (even though their set is not finite) and every real number is not only a product of some addition or subtraction, it also can take part in such an operation.

Polymers make for a special case in which an infinite set (all possible lengths of the polymer) is closed under ligation (but not cleavage, since many cleavings will result in a single monomer which cannot be further cleaved, or even if it were, the products are not a polymer: eventually we would chop the molecule into single atoms which are certainly not members of the set of polymers). In this special case, there canont be any loops, since repeated ligation would simply make longer and longer polymers. That is until we ran out of monomers, having used all the available atoms in the universe. We don't have that problem if we allow at leat some ligation reactions into R.

Clearly (from the polymer ligation example), the abstract notion of closure does not necessarily imply loops, but what of a more practical, material application. Any practical example with chemicals must involve a finite set because chemicals are material things that necessarily run out. Given a finite set and the definition that all members must be reactants and all products must be members of the set (and therefore also reactants), loops become inevitable.  These will be closed loops of material transformations and the set X and its reactions R will be a circular material system. We can summarise them by saying:

Every member of X is material cause for at least one member of X. Since X is a finite set, every member of the set is somehow involved in causing every other member: i.e. loops are inevitable.

A->B, B->C, C->D,...... ,X->something in {A...X} implies that something in {A...X} eventually causes itself.

For example X=(A,B,C,D,E) and A->B, B->C, C->D, D->E, then E must cause one of A, B, C, D or itself. Whatever one is true, it then leads up the chain back to E to form a loop (of course if E->E we have a terminal trivial loop).


Circular material systems

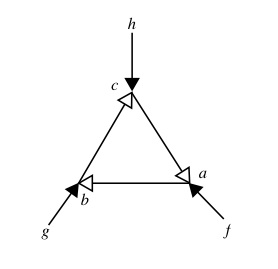Opposite is Fig. 19 from Louie and Pauli (2011) " a closed path of material causation" which is a "sequential cycle" (black headed arrows indicate efficient causality and white headed arrows indicate material causality). So, a, b and c are materials (we may think of them as micro-assemblies of particles whose form, defining them as a particular material, is determined by their formative information). Each is necessary, but not sufficient for creating the next material in the cycle. Not sufficient, because the efficient causes f, g and h are also needed. These can be considered information constraints applied by forms that are not taking part in the cycle, other than as constraining guided for its transformations. They might, for example, be catalysts or schaperone proteins.

Cyclic material causation (circular process causation), in which a set of efficient causes acts on a set of materials to produce a loop of material cause, forms a circular material system.  Catalysis is interpreted as an efficient cause - what makes things happen - and what happens is that materials are transformed, so obviously the (particular) material incredients for the transformation have to engage as reactants, hence the material cause. This is what we see in the autocatalytic sets of Kauffman, Hordijk and Steel.



Circular causal systems

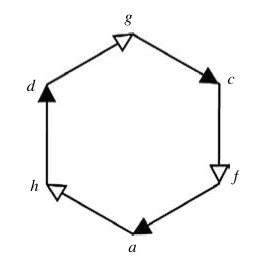Opposite is Fig. 29 from Louie and Pauli (2011): "A hierarchical cycle is the relational diagram in graph-theoretic form of a closed path of efficient causation." Here we see cyclic efficient causation in which efficient causes (black headed arrows) produce material causes (white headed), and all (collectively) are ultimately causes of themselves. Again, thinking of materials as micro-assemblies with associated forrmative information, each in turn constrains whatever is responsible for its following efficient cause (e.g. c constrians the effect of f on a). The efficient causes can be thought of as additional constraining information, which here is itself constrained by the preceeding material cause. The combined effect is ultimate cause: the system causes itself.

Circular causality produces impredicate systems - Rosen's thesis

A predicate is an assertion: what one can say about something, ascribing that thing an attribute or property. To be predicable means being suitable for predicating, i.e. asserting something about. So, impredicate means a thing about which there is nothing one can assert. If a thing exists, why might it be impredicate? In logic and maths, the answer is that it is impredicate if it cannot be defined other than by reference to itself, or a category to which it belongs. It is a sort of generalisation of the "chicken and egg" problem. This is the sense in which circular causality implies impredicativity. Because a circularly causal system causes itself, the answer to the question why does it exist is impredicate.

The classic example of the trouble this can cause is Russell's paradox which arises in the definition of the set of all sets that do not contain themselves.  By definition this set cannot contain itself, so is therefore a member, but it cannot be because only sets that do not contain themselves can be members.... don't loose any sleep over this one (but there is a Wikipedia page about it). The Ouroboros nature of a system that is the efficient cause of itself has not been lost on (at least some Chilean) authors in this field (Soto-Andrade et al, 2011). The Ourorbos is the ancient Egyptian symbol of a snake eating its own tail, later adopted by alchemists and various kinds of weirdness. In almost nightmarish maths, we have f(f)=f  as an expression of a function that, acting on itself, produces itself. Not all Ourorbos dreams are bad:  the structure of benzene was realised by August Kekulé when he dreamt of the atoms  forming  dancing snakes, one of which "seized hold of its own tail" (and if you replace the labels in Fig 29 above with CH, then you would have a benzene ring (with double bonds where the solid arrows are and single bonds otherwise).

Rosen emphasised impredicativity as one of them most important distinguishing features of life, indicitive of the impossibility of creating a 'true model' of a living system. He distinguished between model and mere simulations. The former, being formal systems with the same entailment as the real thing.


Multilevel circularity: The Noble view

We now turn to the question of causation among systems, at least viewed across multiple levels of organisation, especially whether downward causation is compatible with the specific ideas of efficient cause and circularity developed above. For example can a level such as that of whole organism exert efficient causation over one or more of its component subsystems, e.g. metabolic rate, whilst this subsystem in turn exerts efficient causation over the organism. One possibility is that levels of organisation, though they are nested, do not necessarily form an ordered (linear) hierarchy of control. Indeed, we might not be able to tell which level of organisation is primarily determining the system's behaviour, without a detailed examination of its causal structure. Of course if we strictly only believe in bottom-up causation (strict reductionism), then the question does not arise, but we have already established some good reasons to abandon that simplification (see e.g. transcendent complexes).

Denis Noble calls this the principle of biological relativity: " a priori, i.e., before performing the relevant experiments, there is no privileged level of causality " (Noble, 2012). What is meant by circular in his argument (see e.g. (Raymond) Noble et al. 2019) is the combination of upward and downward causation. Upward is seen as the dynamic effect of subsystems on a higher level and downward causation as the constraints set by boundary conditions on the lower level. "Each level of organization provides the boundary and initial conditions for solutions to the dynamic equations for the level below." It is not very clear that the simultaneous action of these upward and downward 'causes' matches the Rosen concept of circular causation we are dealing with in this article.  However, it is clear that biological systems are arranged as nested hierarchies and circular causation in the Rosen sense need not be limited to act in only one of these levels: more likely it spans levels, with constraints from higher levels acting as efficient cause for lower ones and the functional limitations of lower level (components) acting as a sort of efficient cause on the assembly and function of the higher level. Allready, we understand that the labels in the (M,R)-system diagram represent, not elementary entities, but rather subsystems.


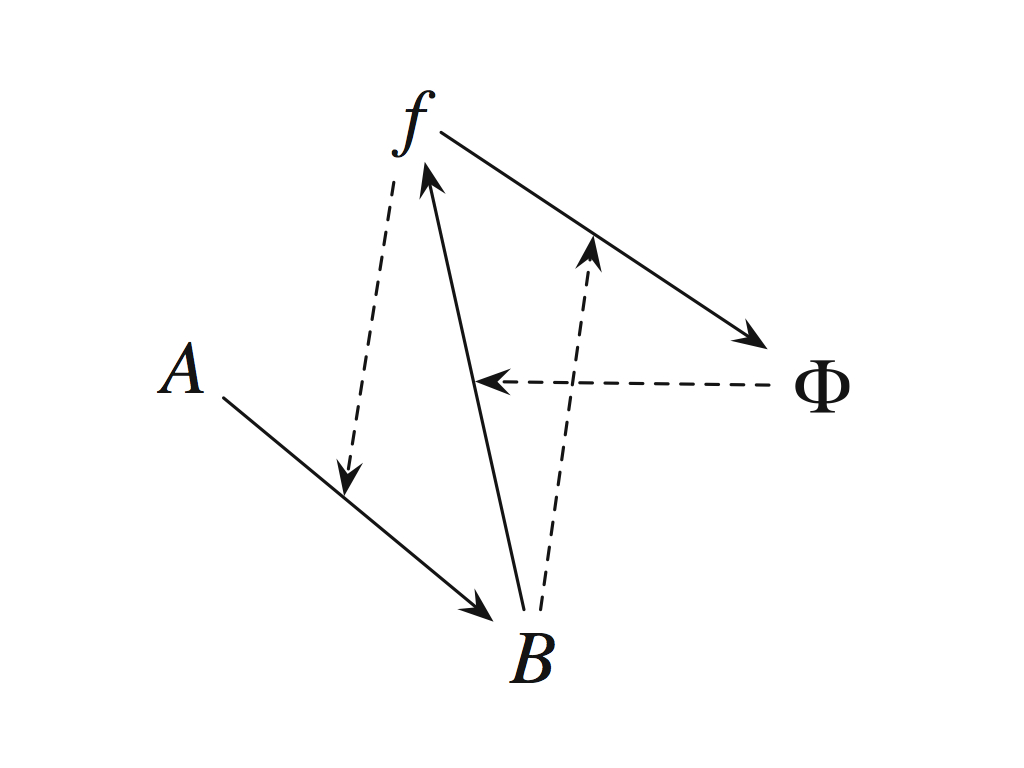
The (M,R)-system redrawn to emphasise its autocatalytic set nature (reproduced from Cárdenas et al., 2010).

A multicellular organism might then be considered as an (M,R)-system of (M,R)-systems in which f and Phi are the physical embodiment of developmental systems. Given this, it is a reasonable possibility that there is no level of organisation that is in overall control, that instead, the circularity of causation spans levels so that they each contribute some of the entailment necessary for overall closure to efficient causation.

The truth is that at this stage we just do not know. It is an exciting prospect to design the investigations that can answer this question (a bit less exciting to face the challenge of obtaining funding to pay for them to be done).


Relation to information

If efficient causation results from (is a phenomenon of) constraint and constraint is quantified by information, then there is reasonable hope of quantifying causation. Not only that, but recasting the phenomenon in information terms removes the problems of 'beginning and end'  inherent in inpredicative systems, so the information approach may be a powerful tool for dealing with circularity of efficeint causation.

Here is an aid to thinking about it. Recall that cause may prevent a change, or movement, just as well as it may produce one. Intuitively, constraints prevent movement. The tremendous strength of stone tower lighthouses lies, to a large extent, in the internal design of tightly interlocking stones. Consider any one of the shaped blocks representing a granite stone in the model of part of the Eddystone lighthouse.


Wooden model of the base of the Eddystone lighthouse, Royal Museum of Greenwich.


The block's form constrains the position and the identity of its neighbouring blocks, so its position has a causal effect on them (again interpreting cause as constraint). Imagine you are building this using the blocks, working clockwise. The neighbouring blocks in turn constrain what you can place next to them and how you orientate them. As you proceed, you will build the circle and eventually place the last blocks, which will be constrained by the ones you started with, but will also constrain the ones you started with: only those ones set in the position you first put them, will fit the pattern. Now with the circle completed, all the blocks constrain each other - there is no begining or end, only mutual constraint.  We can calculate the information embodied by each of the block shapes: it is the amount of information needed to recreate that shape. To this we will add the information needed to specify the coordinates in space where the first block should be placed and the information needed to specify the building of the circle (i.e. place blocks together so they fit) That is just geometry. The shape and placement of the first block dictates all the rest, so all the information embodied by the circle of interlocking blocks is now present and knownable. That information is the same as the information that is creating constraints in the physical world, it is that much information that lies behind the causal structure of the blocks. What it causes is the stregth of the structure (alongside the material cause of the strength of granite - the material from which the real lighthouse was made).

So much for a static system, let us now consider a dynamic one.

References

Louie, AH and Poli, R. (2011). The spread of hierarchical cycles. International Journal of General Systems. 40(3), 237-261

Noble, D. (2012). A theory of biological relativity: no privileged level of causation.
Interface Focus 2, 55–64. doi: 10.1098/rsfs.2011.0067

Noble, R. Tasaki, K., Noble, P.J. and Noble D. (2019). Circular Causality but Not Symmetry of Causation: So, Where, What and When Are the Boundaries?Frontiers in Physiology. 10:827. doi: 10.3389/fphys.2019.00827.

Rosen, R. (1991). Life itself: A comprehensive enquiry into the nature, origin and fabrication of
life. Columbia University Press, New York, USA..

Rosen, R. (2000). Essays on Life Itself. Columbia University Press.

Soto-Andrade, Jaramillo, S., Gutiérrez, C. and Letelier, J-C. (2011). Advances in Artifical Life, ECAL 2011: Proceedings of the 11th European Conference in the Synthesis and Simulation of Living Systems. MIT Press. pp 763-770.

Back to the Biocomplexity Theme |