Understanding concepts of Closure

A short article by Keith Farnsworth and probably the only one on the worldwide web which deals with this topic. (Jan. 2022)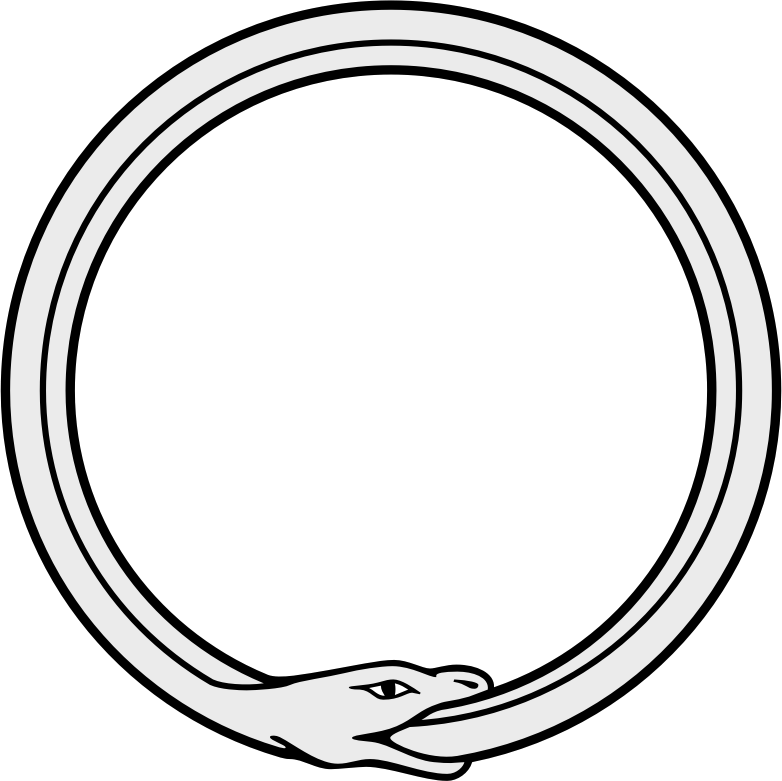


Closure is a concept that crops up a lot in the organisational theory of biology. It turns out to be one of the most important characteristics of living systems and one that in some respects defines life itself. At a simple practical level, it means turning a linear chain of events, or causes and effects, back on itself to form a loop. More generally it describes a loop of relationships among objects. The quintessential symbol of closure is the Ouroboros (a snake eating its own tail). It is the metaphor for cyclic, endless, recursion. The, rather weird, equation f(f)=f is a very compact mathematical expression of the idea. Its relation to understanding what life is and how it works is elaborated in the conference paper by Soto-Andrade et al. 2011. In the equation, f is a function which when operated on itself produces itself. This inherently breaks the distinction between operator and operand - between verb and object. That is a fundamental of life - the process of living and the organism doing the living are the same: living is a process, the outcome of which is itself. Even more fundamentally, it is the recursive relationship behind the embodiment of information in a particular configuration of matter, that is configured (that particular way) by the very same information that it embodies.

This may seem a little arcane, but it turns out to be tremendously important for precisely working with causality and autonomy. In particular, a Kantian whole may be more precisely defined as a system with transitive causal closure. To understand this, we will start with the definition of closure in general, this leads directly to operational closure, with which we explain transitive closure and then identify organisational closure, finishing with closure to efficient causation.

The simplest and most concise, but general, way I can think of to express the idea of closure is this:  consider a set of objects; whatever you do to them, you can only get members of the same set from doing it.

It applies for very constrained circumstances - for example, if A is the set of pieces of vegetable, and c is to chop, then A is closed under the operation c. That is no matter how much you chop members of A (pieces of vegetable), what you get is just more members of A. In other words chopping will not get you out of the set A, so the set is closed under c.

The idea also applies to very big and general categories. Most significant is the case of causal closure. This is the idea that every event in the physical world is caused by an event in the physical world. That is if E is the set of physical events, then there is nothing that can can happen in E that can take you out of E and nothing beyond (outwith) E that has any bearing on E. In this way, the concept of closure carries the notions of completeness and sufficiency: all that is needed, all accounted for and nothing else. The closure refers to the set of objects (not the objects themselves, which may be real things, or concepts or anything) under operations permitted with that set. So physical causal closure means that the universe is a closed system in which physical things, such as atoms and photons, can only be influenced by other physical things and in turn can only influence other physical things. This idea is also called the causal completeness of physics, which should be self-explanatory.

[Incidentally, this, seemingly undemanding, restriction has become a major controversy in the philosophical debate over free will, because some contend that if it is true, then mental (non-physical) causes are impossible, which in turn means if all physical causes have prior causes, free will is impossible. The informationist organisational approach favoured on this website provides a satisfying solution to that problem which philosophers (by and large) are unaware of. More about that later.]

To get an intuitive grasp of closure, imagine a group of people, let us say they are all members of the class studying environmental biology at Queen's University Belfast (my students). Among them is a subset who have entered a pact - that they will only ever speak to, listened to, or otherwise engage with one another, never anyone else. Certainly this lot have become a closed group. Can another person be a part of that sect? No because they will never be able to engage any of the existing members to make an application, or be taken notice of at all. Can there be any member of the sect that engages with anyone beyond the sect? - of course not, by definition (and if they were found to have done so they would be immediately expelled and never spoken to again). Finally, is it possible for a member of the sect to never engage with any member of the sect? That is more difficult, but technically, they are not really part of the sect, so not a member of the closed set of people in the pact because they don't fulfill all the criteria of membership. That is, we cannot say that they only ever interact with other members of the set, because actually they don't interact with any of them. Technically they are in another set - that of people who never engage with anyone at all under any circumstances.  Here is a video that explains it in a simple mathematical context.


More formally:

Closure: is a mathematical concept applying to sets of relations. In general, a set ‘has closure under an operation’ if performance of that operation on members of the set always produces a member of that same set: this is the general definition of operational closure. If the operation is relational (relating one element of the set to another, e.g. A>B), then the system has relational closure if it has operational closure under the relational operator. Mathematicians will say that the set of real numbers is closed to addition because the relational operation a + b, where a and b are both real numbers always produces another real number. In this sense closure implies that one cannot get out of the set, no matter how devious and complicated one chooses combinations of the operation. The set of real numbers is obviously not closed under the operation of taking the square root, since negative numbers are real and the square root of them is not (and this is equivalent to multiplying by i (the square root of -1)), so the outcome takes us out of the set.

This idea can be applied in many relevant systems, it is certainly not just for numbers.
For example: if X is a set of chemical species and R a set of reactions, then if for every possible reaction in R among members of X, the products are always also members of X, then the set X is closed under R (this is one of the prerequisites of autocatalytic sets).


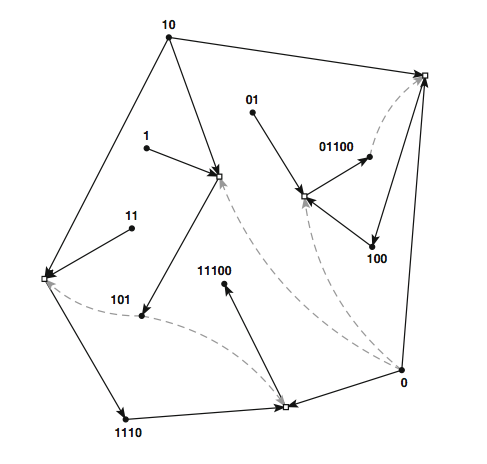
In Kauffman's autocatalytic sets, every object (a binary word) is either an ingredient for another, a product of a reaction on two others and may also be a catalyst for one of the reactions. That way all the binary word objects are members of a set that is closed under the set of reactions among them. Here the reagents are shown with solid arrows pointing to the reactions, from which solid arrows point to the products, whith dashed grey arrows indicating the catalytic effects of other objects within the set. Clearly everything in this set of binary words is either made by or makes another member of the set, so the set of words is closed under the set of reactions.





Relational closure is immediately useful in thinking about cause and effect. Let A->B denote A causes B. Then, A->B and B->C implies that A->C. That is, of course, true for arbitrary lengths of causal chain: A->B->C->D->E->F implies A->F. This also means that causal chains of this kind are transitive.

Transitive closure. In maths, if A->B and B->C then the set {A B C} is transitive only if A->C, where the arrow -> represents any relation between the elements. The most obvious one is 'greater than': A > B and B > C, so (because > is transitive) A >C. This is often applied to directed graphs: diagrams that show the directional relations among objects, such as the flight connections among airports. We could have Dublin links to London and London links to Dundee. If there is no direct link between Dublin and Dundee, this set of airports is not transitive under flight connections. We could make the set transitive by adding a connection between Dublin and Dundee.


We can apply this to constraints.
If we interpret the arrow A->B as meaning A constrains B, then transitive closure defines a kind of causal chain. This is very useful when challenged to account for circular causality. As we just saw, causation is supposed to be transitive, so a loop such as A causes B causes C causes A should be impossible. Yet that is exacltly what autopoiesis and 'closure to efficient causation' claims to be the case.

In the more general and realistic language of constraints: A->B->C->A implies that A sets limits on the behavioural repertoire of B, that in turn limits the behaviour of C and that limits A. We might say that the constraint on A by C is limited by A itself, using B as an intermediary. This turns out to be a very common template of biological control systems.

Constraint is already intuitively a kind of causation, but deeper thinking reveals it to be the very essence of causation. That is because the normal idea of causation coincides with Aristotle's efficient cause and that is the result of form constraining physical forces. Here, the meaning of 'form' is the space-time configuration of the fundamental particles that produce the forces (this is explained in the physical basis of cause). The configuration (form) is an embodiment of information and information is equivalent to constraint (because the more informed a system is, the fewer its  degrees of freedom: see entropy for explanation of that).

So despite it seeming impossible for a thing to be the cause of itself, it turns out to be easy to show that a thing can, via a set of relations, constrain itself. If constraints are transitive (and I believe they must be), then A->B->C->A implies A<-B<-C<-A as well, or more succinctly, everything constrains everything, including itself.


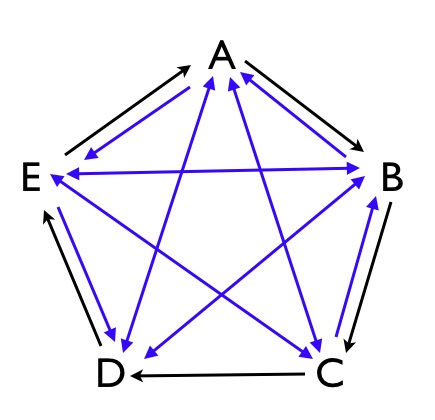
We can see the use of this when looking at the diagram on the left, which shows constraints among five configurations (objects such as molecules). The constraints are shown as black arrows with a direction indicating which configuration constrains which. If we then stipulate that the constraints are transitive, then we have to introduce the blue arrows, (several of which are two-way constraints). This results in a system of configurations which all constrain one-another. This set of configurations is therefore closed under constraint. That is the organisational structure of e.g. Hofmeyr's self-manufacturing cell featured here. More generally, since constraint is an operation, the system is operationally closed (specifically with respect to constraint).






The mathematical idea of operational closure was used in the ‘Closure Thesis’ (post-hoc, by the way) underpinning Maturana and Varela's theory of autopoiesis. They said that "every autonomous system is operationally closed". 

[This, though, is a curious logic, since for self-construction it is only necessary that every part of the system is the result of operations on only parts of the system, leaving open the possibility that some operations of the system may result in things that are not part of the system. That is, it does not matter if the system's operation produces by-products that are not a part of the system (e.g. waste matter), as long as all the parts of the system are produced by what are already parts of the system, as opposed to anything beyond the system.]


Organisational closure. According to Heylighen (1990), “In cybernetics, a system is organisationally closed if its internal processes produce its own organisation” (my emphasis).
What does it mean to produce organisation? Well, organisation is the result of constraint: the more constraints applied to an assembly, the more organised it gets, in the sense that as its degrees of freedom are closed off, it becomes more certainly in any particular configuration, or to put it another way, as the number of possible configurations decreases, the assembly embodies more information. So producing organisation is the same as applying constraints and also the same as embodying information. So Heylighen is saying that if a cybernetic system is organisationally closed, it means the information which gives it that organisation arose from the constraints applied by that same organisation  (you can see why the ouroboros is a good representation of this sort of thing).


This mathematical idea was used in the ‘Closure Thesis’ (post-hoc, by the way) underpinning Maturana and Varela's theory of autopoiesis.  Quoting Varela (1974) “A domain K has closure if all the operations defined in it remain with the same domain. The operation of the system has therefore closure, if the results of its action remain within the system itself". More loosely, Vernon et al. (2015) stated that “the term operational closure is appropriate when one wants to identify any system that is identified by an observer to be self-contained and parametrically coupled with its environment but not controlled by the environment. On the other hand, organizational closure characterizes an operationally-closed system that exhibits some form of self-production or self-construction”. In other words, organisational closure was the term chosen by the Santiago school to describe autopoiesis in general, rather than specifically in the case of life, for which obviously autopoiesis was already the term. That left operational closure to refer to any system that is closed in the mathematical sense to control relations: hence not controlled by its environment. 


Causal closure.
Rosen (1991 and many articles preceding) used the Aristotelean language to describe the special case of causal closure, calling it “closure to efficient cause”. This is an operational closure in which the operation is specifically causal (meaning efficient cause) - see circular causation.

This idea was formalised by a mereological argument (mereology deals with parts and wholes with formal logic) in Farnsworth (2017) to define systems with an inherent cybernetic boundary (i.e. where inside is definitively separate from outside) as only those systems that have transitive closure for causation, (xCy: read as x causes y, meaning that the state of an object y is strictly determined by the state of the object x). The transitive causal closure of a system means that its  components form a set A of causally related objects under C such that there is no object in A who’s  state is not caused by an object in A: every part of the system is causally connected to every other.
It is from such systems that a transcendent complex may arise. Finally, taking causation as manifest in mutual information, Bertschinger et al. (2006) derived a quantitative metric of information closure to  operationalise these concepts in systems theory, which has developed into an information-theoretic  method for system identification (Bertschinger et al. 2008).

I say finally, but should now add that Larissa Albantakis has put the metric of Bertschinger et al. (2008) together with several other proposed metrics of cybernetic (control circuit) closure in a progressive review of ways to characterise system autonomy.

Closure to Efficient Causation

This terminology is now taken to mean ontological closure (the making of oneself), i.e. autopoiesis, which is unique to living systems and has been particularly developed through the relational biology, started by Rashevski, developed by Robert Rosen and his followers, most notably Aloisius Louie. In words it means that every part of the system is made by the actions of the system as a whole. The meaning of made here is both fabrication and assembly of the parts. Both of these are enacted by efficient causation, which, as explained in the physical basis of cause, is information constraining physical forces.

A little more technically, The term closure to efficient causation refers to a property of hierarchical cycles, following Rosen (1985), in which the hierarchy refers to the containment of one efficient cause within another. This is fully worked out in Section 3.3 of my paper "How an information perspective helps overcome the challenge of biology to physics". In there, I illustrate the use of causal analysis to describe the causal structure of the ATP-synthase complex and find it is far from being closed to efficient causation.

Readers may also take note of (and contrast closure to efficient causation) with the sequential cycle having closure to material cause, e.g. the great bio-geo-chemical cycles of the earth: the nitrogen cycle, carbon cycle, etc. The essential difference is that these rely on pre-existing formal cause (information embodied as physical form) to work, wheras a system that is closed to efficient cause is responsible for the instantiation of all the information that gives it the form to organise the material cycle. That is why systems with this property typically appear as alternating efficient and material causes linked in a circle that reminds us of the ouroboros that we see at the top of this page.


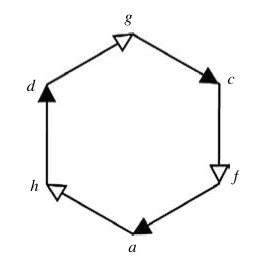
A hierarchical cycle (from Louie and Poli, 2011). Solid arrows show efficient cause and hollow arrows show material cause. This can be read, starting at a, as material transformation from a to h is caused by efficient cause (f to a) which is generated by f that is the result of a material transformation from c, caused by efficient cause g to c, that is generated by g from the product of material transformation from d to g that is caused by efficient cause h which is generated by the material transformation from a to h. In detail, the generation of an efficient cause is the constraint of physical forces from the material (substance) by its form (formal cause) which is information embodied as a particular configuration of e.g. atoms. The physical forces are usually the electrostatic forcefields generated by the electron clouds of atoms that give rise to chemistry, including all the biochemical processes we are familiar with such as binding, cleaving, hydrophilic and hydrophobic forces, hydrogen bonds etc..



References.

Albantakis, L. Quantifying the Autonomy of Structurally Diverse Automata: A Comparison of Candidate Measures. Entropy (2021). 23,1415. https://doi.org/10.3390/ e23111415


Bertschinger, N.; Olbrich, E.; ay, N.; Jost, J. Information and closure in systems theory. German Workshop on Artificial Life <7, Jena, July 26 - 28, 2006>: Explorations in the complexity of possible life, 9-19 (2006), 2006.

Bertschinger, N.; Olbrich, E.; ay, N.; Jost, J. Autonomy: An information theoretic perspective. Bio Systems 2008, 91, 331–45.

Farnsworth, K.D. Can a robot have free will? Entropy 2017.

Heylighen, F. Relational Closure: a mathematical concept for distinction-making and complexity analysis. Cybernetics and Systems 1990, 90, 335–342.

Hofmayr, J-H. S. A biochemically-realisable relational model of the self manufacturing cell. (2021). Biosystems. 207:104463. doi:10.1016/j.biosystems.2021.104463

Hordijk, W.; Steel, M. Detecting autocatalytic, self-sustaining sets in chemical reaction systems. J. Theor. Biol. 2004, 227, 451–461.

Kauffman, S.A. Autocatalytic sets of proteins. J. Theor. Biol. 1986, 119, 1–24.

Kauffman, S.A. Origins of Order: Self-Organization and Selection in Evolution; Oxford University Press: Oxford, UK, 1993.

Kauffman, S.A. Investigations; Oxford University Press, 2000.

Louie, AH and Poli, R. (2011). The spread of hierarchical cycles. International Journal of General Systems. 40(3), 237-261

Moreno, A.; Mossio, M. (2015)   Biological Autonomy: A Philosophical and Theoretical Enquiry. In History, Philosophy and Theory of the Life Sciences; Springer: Dordrecht, The Netherlands.  Volume 12.

Mossio, M.; Bich, L.; Moreno, A. Emergence, closure and inter-level causation in biological systems. Erkenntnis 2013, 78, 153–178.

Rosen, R., (1985). Organisms as causal systems which are not mechanisms: An essay into the nature of complexity, in: Rosen, R. (Ed.), Theoretical Biology and Complexity. Academic Press. chapter 3, pp. 165 – 203.

Rosen, R. Life itself: A comprehensive inquiry into the nature, origin and fabrication of life; Columbia University Press: New York, USA., 1991.

Soto-Andrade J, Jaramillo S, Gutiérrez C, Letelier JC (2011) Ouroboros avatars: a mathematical exploration of self-reference and metabolic closure. In: Lenaerts T, Giacobini M, Bersini H, Bourgine P, Dorigo M, Doursat R (eds) Advances in artificial life, ECAL 2011: proceedings of the eleventh European conference on the synthesis and simulation of living systems. The MIT Press, Cambridge, pp 763–770. http://personales.dcc.uchile.cl/~cgutierr/papers/ecal2011.pdf


Varela, F.; Maturana, H.; Uribe, R. Autopoiesis: the organization of living systems, its characterization and a model. Curr. Mod. Biol. 1974, 5, 187–96.

Vernon, D.; Lowe, R.; Thill, S.; Ziemke, T. Embodied cognition and circular causality: on the role of constitutive autonomy in the reciprocal coupling of perception and action. Frontiers in psychology 2015, 6.