Biodiversity as Information Density
From Sample Diversity to Information Fields
The
traditional notion of biodiversity considers a sample taken by field
ecologists using a fixed area (a quadrat). Within the area there is a
sample of the whole community being studied and by fully quantifying
some aspect of diversity in this area (if it is representative of the
whole) an estimate of the community diversity is obtained. Of course
this estimate is made more accurate and precise by increasing the area
of the sample, or equivalently, adding more samples to form a pooled
sample. The simplest measure is a count and the count of species
present in the sample is called the species richness - this is still
the most common measure of biodiversity found in the literature. A
single sample (perhaps composed of multiple quadrats, pooled) gives a
localised measure of species richness, termed the alpha-diversity. If
there are two or more alpha-diversity estimates, then the diversity
among them is termed the beta-diversity.
Unfortunately, there are many
ways to define precisely what this means, but all amount to quantifying
the difference among alpha-samples and expressing it as a proportion of
the average diversity within them. The combined diversity of all the
quadrats used to calculate beta-diversity, when pooled, is termed the gamma-diversity: it is
equivalent to the alpha-diversity of the whole
area sampled. It is important to note at this point that all these
traditional measures describe samples of the biological system, not the
system itself (though they do imply something about it). For example,
if we think of an ecological community lying over an environmental
gradient (perhaps running from the valley floor to the top of a
mountain), then the alpha-diversity at one end will in general be
different from the other end. Further, because each end contains a
different (but maybe overlapping) set of organisms, there will be a
more or less high beta-diversity among samples taken from each end.
This means, in turn, that the gamma-diversity of the whole system is
relatively high, but notice that the beta-diversity among adjacent
alpha-samples will be small: in fact beta-diversity is a continuous
variable of the physical distance among alpha-samples.
All this suggests a more general outlook is needed - one which describes the diversity ‘density’ over the surface.
This notion is analogous to the potential difference which can be calculated over an electrical field. At each point in the field, there is an electrical potential and variation in space of the potential gives a local gradient which can causes an electro-motive force. Strictly at a singular point, there is no gradient, but it can be defined by the local gradient via differential vector calculus - the ‘div’, ‘grad’ and ‘curl’ which do the same job in flow equations such as for heat and fluid mechanics and beautifully summarise electrical and magnetic fields in Maxwell's equations). The local diversity around a point in space gives us a gradient measure in diversity. That is hard to envisage, but if we recall that diversity is a measure of difference and that difference is fundamentally information content, then we have a local gradient in information, which in turn can be described as a field (analogous to that of the electrical potential). This more general view, then describes biodiversity which extends over space, as a field of information density (and it can be three as well as two dimensional). Alpha-diversity then becomes an estimate of the diversity in a small region, obtained from integrating over the region (surface area, or for aquatic and soil systems, perhaps a volume). In practice the integration can be replaced with a summation. The beta-diversity is then re-interpreted as a gradient measure, which in general will have a direction, hence a ‘div’, ‘grad’ and ‘curl’ are needed to describe it.
What is more, this information-density interpretation enables us to freely move from counts of species, or functional groups of organisms, to estimates of the information content of life in the area. In this way, the alpha-diversity of a monoculture of simple bacteria will be less than that of a single vertebrate, or a complex community of bacteria (which may anyway be living inside the vertebrate). On the mountainside, the information density will probably have a larger gradient up the slope of the mountain, than around any contour line on the map: the beta-diversity will be quantified with a direction, over the whole space and independently of scale. At present, this information field notion of biodiversity is just a suggestion - it has yet to be put into practice.
All this suggests a more general outlook is needed - one which describes the diversity ‘density’ over the surface.
This notion is analogous to the potential difference which can be calculated over an electrical field. At each point in the field, there is an electrical potential and variation in space of the potential gives a local gradient which can causes an electro-motive force. Strictly at a singular point, there is no gradient, but it can be defined by the local gradient via differential vector calculus - the ‘div’, ‘grad’ and ‘curl’ which do the same job in flow equations such as for heat and fluid mechanics and beautifully summarise electrical and magnetic fields in Maxwell's equations). The local diversity around a point in space gives us a gradient measure in diversity. That is hard to envisage, but if we recall that diversity is a measure of difference and that difference is fundamentally information content, then we have a local gradient in information, which in turn can be described as a field (analogous to that of the electrical potential). This more general view, then describes biodiversity which extends over space, as a field of information density (and it can be three as well as two dimensional). Alpha-diversity then becomes an estimate of the diversity in a small region, obtained from integrating over the region (surface area, or for aquatic and soil systems, perhaps a volume). In practice the integration can be replaced with a summation. The beta-diversity is then re-interpreted as a gradient measure, which in general will have a direction, hence a ‘div’, ‘grad’ and ‘curl’ are needed to describe it.
What is more, this information-density interpretation enables us to freely move from counts of species, or functional groups of organisms, to estimates of the information content of life in the area. In this way, the alpha-diversity of a monoculture of simple bacteria will be less than that of a single vertebrate, or a complex community of bacteria (which may anyway be living inside the vertebrate). On the mountainside, the information density will probably have a larger gradient up the slope of the mountain, than around any contour line on the map: the beta-diversity will be quantified with a direction, over the whole space and independently of scale. At present, this information field notion of biodiversity is just a suggestion - it has yet to be put into practice.
Scale,
Course Graining and
Quantisation
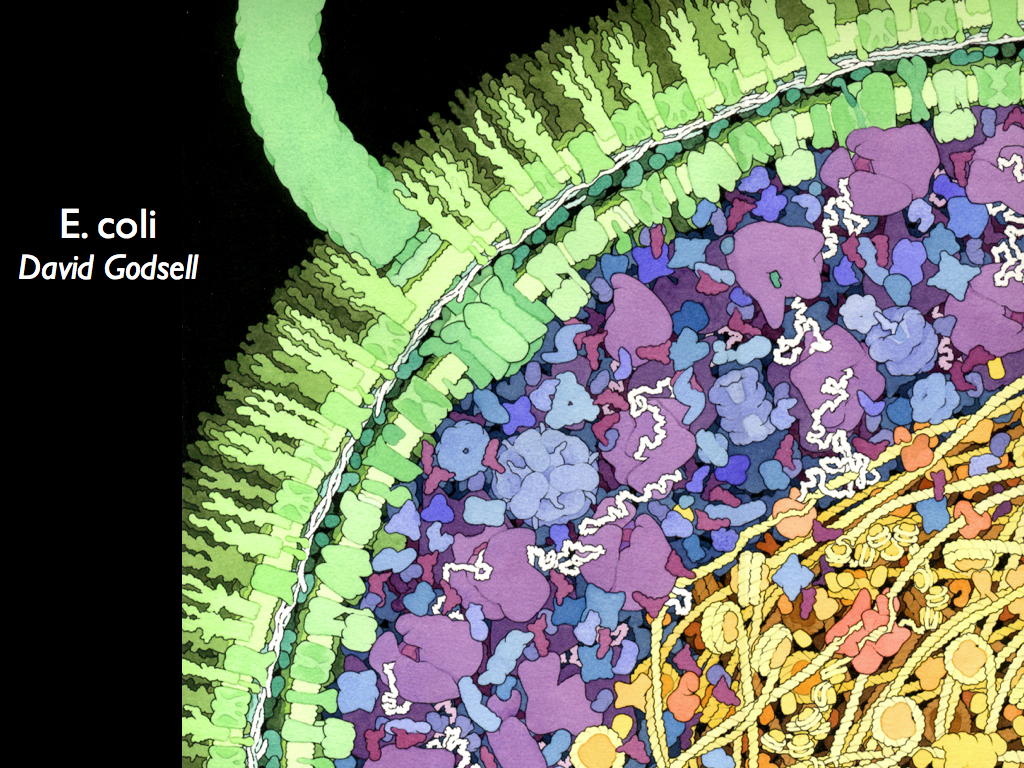
Since information is difference, there must be at least two distinct things to be different from each other and this sets a minimum scale and quantisation for diversity when it is interpreted as information density. But this minimum is too small to matter in practice: two atoms of different elements will be enough. We will probably never want to quantify biodiversity at the atomic scale and might reasonably argue that life does not exist at that scale anyway: given the definition of life that we are working towards, it might admit large molecules and complexes such as the nano-machines found in cells, but that is probably as small as we would ever go. A reasonable example of this might be the 'proteome' of a cell (proteome is the collection of proteins expressed and therefore present). There would be a diversity of proteins in the membranes, cytoplasm, organelles (if present) and inter-cellular space. We might then consider this to be the deepest level of biodiversity, existing at the finest scale of resolution (like the pixels in a digital image). If we look again at the image of part of an e-coli bacterium by David Godsell, we can easily imagine a moving frame (quadrat) scanning over it and quantifying the number of, and degree of, differences among proteins as it moves over the image. From this, information could be quantified using the principles of entropy accounting and a map of information density could be constructed to represent the bacterium in bio-information terms.
Since information is difference, there must be at least two distinct things to be different from each other and this sets a minimum scale and quantisation for diversity when it is interpreted as information density. But this minimum is too small to matter in practice: two atoms of different elements will be enough. We will probably never want to quantify biodiversity at the atomic scale and might reasonably argue that life does not exist at that scale anyway: given the definition of life that we are working towards, it might admit large molecules and complexes such as the nano-machines found in cells, but that is probably as small as we would ever go. A reasonable example of this might be the 'proteome' of a cell (proteome is the collection of proteins expressed and therefore present). There would be a diversity of proteins in the membranes, cytoplasm, organelles (if present) and inter-cellular space. We might then consider this to be the deepest level of biodiversity, existing at the finest scale of resolution (like the pixels in a digital image). If we look again at the image of part of an e-coli bacterium by David Godsell, we can easily imagine a moving frame (quadrat) scanning over it and quantifying the number of, and degree of, differences among proteins as it moves over the image. From this, information could be quantified using the principles of entropy accounting and a map of information density could be constructed to represent the bacterium in bio-information terms.